基本介紹
正弦型函式是實踐中廣泛套用的一類重要函式,指函式y=Asin(ωx+φ)(其中A,ω,φ均為常數,且A>0,ω>0)。這裡A稱為振幅,ω稱為圓頻率或角頻率,φ稱為初相位或初相角,正弦型函式y=Asin(ωx+φ)是周期函式,其周期為2π/ω。
正弦型函式的圖像
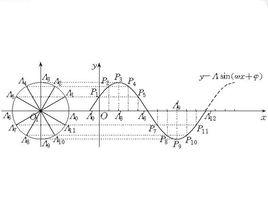
正弦型函式y=Asin(ωx+φ)圖象的幾何畫法是:在橫軸Ox上任取一點C為圓心,A為半徑作圓,與x軸相交於兩點A和A.以A為始點,任意等分此圓(圖中是12等份),設分點為A(i=0,1,2,…,12),其中A與A重合,在x軸上取OA′=-φ/ω,然後從A′起作A′(i=0,1,2,…,12),使A′A′=π/6ω,即周期2π/ω的1/12,過A與A′分別與x軸和y軸平行的直線交於點P,連結P各點成光滑曲線,即得y=Asin(ωx+φ)在一個周期內的近似圖象。正弦型函式的圖象也稱為 正弦型曲線或稱 正弦波。如圖1所示。
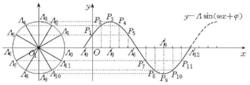 圖1
圖1 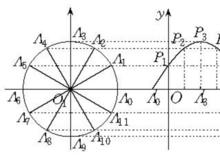 圖1(a) 圖1(a) | 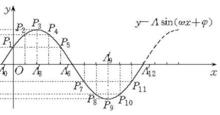 圖1(b) 圖1(b) |
正弦型曲線還可由正弦曲線y=sin x的圖象經過適當的橫向和縱向的伸縮變換及橫向平移變換而得到,許多物理現象的規律可以用正弦型函式表示,如質點作簡諧振動時,該質點相對於平衡位置的位移y與時間t的關係可用正弦型函式表示。羅貝瓦爾(G.P.de.Roberval)於1634年在研究旋輪線時,把正弦型曲線y=a sin(x/a)(其中a是母圓的半徑)當做旋輪線的伴侶而引入數學的。
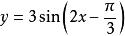 正弦型函式
正弦型函式例 如函式 的圖像也可以利用正弦曲線y = sinx經過圖像變換得到:
(1)把正弦曲線y= sinx上的所有點的橫坐標縮小到原來的一倍(縱坐標不變),得到函式y= sin2x的圖像。
 正弦型函式
正弦型函式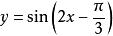 正弦型函式
正弦型函式(2)再把函式y=sin2x的圖像上的所有點向右平移 個單位長度,得到函式 的圖像。
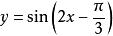 正弦型函式
正弦型函式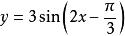 正弦型函式
正弦型函式(3)再把函式 的圖像上所有點的縱坐標擴大到原來的3倍(橫坐標不變),就得到函式 的圖像(圖2) 。
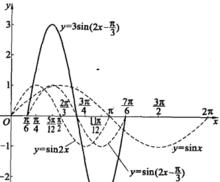 圖2
圖2由於函式y=Asin(ωx+φ)(其中A,ω,φ都是常數,A、ω∈R )的圖像可以由正弦曲線經過變換得到,因而這樣的函式稱為正弦型函式,其圖像稱為正弦型曲線。
正弦型函式的性質
正弦型函式y=Asin(ωx+φ)(其中A,ω,φ均為常數,且A>0,ω>0)有如下性質:
(1) 定義域 y=Asin(ωx+φ)定義域為x∈R。
(2) 值域 y=Asin(ωx+φ)值域為[-A,A]。
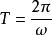 正弦型函式
正弦型函式(3) 周期性 y=Asin(ωx+φ)周期 。
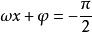 正弦型函式
正弦型函式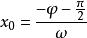 正弦型函式
正弦型函式(4) 單調性 設 ,求出 ,
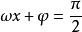 正弦型函式
正弦型函式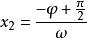 正弦型函式
正弦型函式設 ,求出 ,
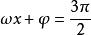 正弦型函式
正弦型函式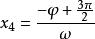 正弦型函式
正弦型函式設 ,求出 ,
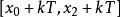 正弦型函式
正弦型函式y=Asin(ωx+φ)在 (k∈Z)上是增函式:
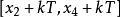 正弦型函式
正弦型函式y=Asin(ωx+φ在 (k∈Z)上是減函式。
(5) 奇偶性 在y=Asin(ωx+φ)中,當φ=0時,是奇函式;當φ≠0時,既不是奇函式,也不是偶函式 。