定義
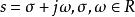 正實函式
正實函式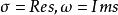 正實函式
正實函式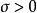 正實函式
正實函式 正實函式
正實函式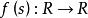 正實函式
正實函式 正實函式
正實函式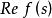 正實函式
正實函式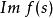 正實函式
正實函式 正實函式
正實函式設 s為一個複數, s可寫成也可寫成,表示具有正實部,稱為 實函式,如果。儘管是個實函式,但是當 s是複數時,它的值通常是複數。用和分別表示的實部和虛部。
 正實函式
正實函式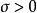 正實函式
正實函式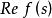 正實函式
正實函式實函式稱為 正實函式,如果,就有。
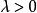 正實函式
正實函式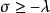 正實函式
正實函式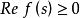 正實函式
正實函式 正實函式
正實函式如果存在,當時,,則稱是一個 嚴格正實函式。
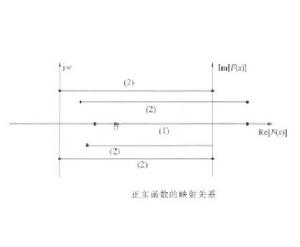
粗略地講,一個正實函式就是將複平面上的實軸映射到實軸,將右半複平面映射到右半複平面。
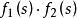 正實函式
正實函式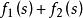 正實函式
正實函式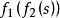 正實函式
正實函式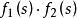 正實函式
正實函式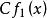 正實函式
正實函式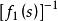 正實函式
正實函式從定義出發容易得到結論:如果是兩個正實函式,那么和也是正實的;但是未必是正實的。當C是正數時,也是正實的;另外也是正實的。
相關性質定理
下面兩個定理刻畫了正實函式和嚴格正實函式的特徵,它們可以用複變函數知識來證明。
定理1
 正實函式
正實函式實函式是正實的充分必要條件是下面三條同時滿足:
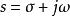 正實函式
正實函式 正實函式
正實函式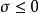 正實函式
正實函式(1)如果是的極點,則;
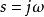 正實函式
正實函式 正實函式
正實函式(2)如果是的極點,則它是單重的.並且 留數為非負數;
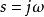 正實函式
正實函式 正實函式
正實函式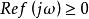 正實函式
正實函式(3)如果不是的極點,則。
定理2
 正實函式
正實函式實函式是嚴格正實的充分必要條件是下面兩條同時滿足:
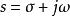 正實函式
正實函式 正實函式
正實函式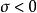 正實函式
正實函式(1) 如果是的極點,則;
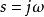 正實函式
正實函式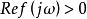 正實函式
正實函式(2) 對任意的,。
 正實函式
正實函式 正實函式
正實函式 正實函式
正實函式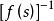 正實函式
正實函式 正實函式
正實函式定理1的第一個條件是說在開的右半複平面沒有極點,我們將這個事實說成在開的右半複平面解析。如果是正實的.那么]也是正實的,那么在開的右半複平面也沒有零點,所以一個正實函式在開的右半複平面沒有零極點。因而定理1中的(2)和(3)中的“非負”都可以改為“正”。同理可得,一個嚴格正實函式在閉的右半複平面沒有零極點。
定理3
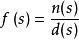 正實函式
正實函式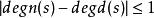 正實函式
正實函式如果有理函式是正實的,那么。
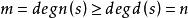 正實函式
正實函式證明:不妨設,那么用帶餘除法得到
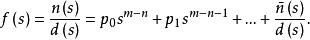 正實函式
正實函式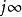 正實函式
正實函式 正實函式
正實函式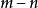 正實函式
正實函式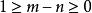 正實函式
正實函式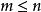 正實函式
正實函式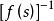 正實函式
正實函式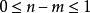 正實函式
正實函式因此是的重極點,根據定理1中(2).虛軸上的極點最多是一重的,因此。如果,那么討論,同理可得。結論獲證。
定理4
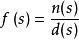 正實函式
正實函式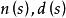 正實函式
正實函式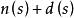 正實函式
正實函式如果有理函式是嚴格正實的,那么和都是Hurwitz多項式。
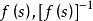 正實函式
正實函式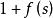 正實函式
正實函式證明:將定理2的(1)用於和,結論立得。
性質1
正實函式的倒數仍為正實函式。
性質2
正實函式之和仍為正實函式。
性質3
正實函式的複合函式仍為正實函式。
例題解析
考慮函式
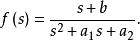 正實函式
正實函式討論它是嚴格正實函式的條件。
 正實函式
正實函式解:要求是嚴格正實的,因此分子和分母都是Hurwitz多項式,所以得到
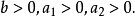 正實函式
正實函式 正實函式
正實函式 正實函式
正實函式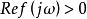 正實函式
正實函式要使得是嚴格正實的,只要對所有成立。因為
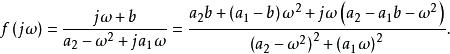 正實函式
正實函式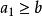 正實函式
正實函式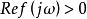 正實函式
正實函式 正實函式
正實函式 正實函式
正實函式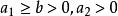 正實函式
正實函式所以只要就有對一切成立。總之,是嚴格正實的條件為:。