概念
正交配置法(Orthogonal Collocation Method),是加權餘項法(Method of Weighted Residuals)的一種,可用於解線性以及非線性常微分方程組、偏微分方程組的初值和邊值問題。該方法特別適合求解非線性問題,與傳統差分法相比,具有計算精度高和穩定性好等優點。
所謂加權餘項法,是將微分方程的未知解展開成一組具有可調常數的試驗函式,選擇合適的常數值,使得試驗函式充分接近於微分方程的精確解。若選用正交多項式為試驗函式,並取正交多項式的根作為配置點時,則稱為正交配置法。
基本原理
在實際套用中,求解區域常為對稱的,如為平板、圓柱、圓球,此時可構造如下的試驗函式:
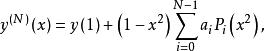 正交配置法
正交配置法該式滿足:
 正交配置法
正交配置法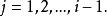 正交配置法
正交配置法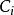 正交配置法
正交配置法式中 為常數,且
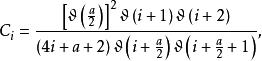 正交配置法
正交配置法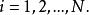 正交配置法
正交配置法滿足上式的多項式即Jacobi多項式。
正交多項式的零點,即配置點,根據Villadsen和Stewart的研究,用配置點處的解 進行計算,可以提高計算效率,簡化電腦程式,試函式的數值導數可以表示為如下:
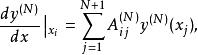 正交配置法
正交配置法 正交配置法
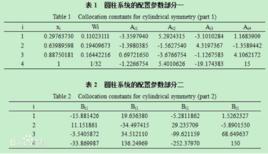
正交配置法對於圓柱對稱系統,當配置點數N=3時,上述各參數如表1所列:
 正交配置法 正交配置法 |  正交配置法 正交配置法 |  正交配置法 正交配置法 | 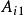 正交配置法 正交配置法 |  正交配置法 正交配置法 | 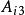 正交配置法 正交配置法 | 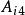 正交配置法 正交配置法 |
| 1 | 0.29763730 | 0.11023111 | -3.3597940 | 5.2924315 | -3.1010284 | 1.1683909 |
| 2 | 0.63989598 | 0.19409673 | -1.3980385 | -1.5627540 | 4.3197367 | -1.3589442 |
| 3 | 0.88750181 | 0.16442216 | 0.69721650 | -3.6766754 | -1.1267583 | 4.1062172 |
| 4 | 1 | 1/32 | -1.2266754 | 5.4010626 | -19*.174383 | 15 |
將上述各參數帶回待求偏微分方程(組),原方程轉化為常微分方程組,此時即可用Runge-Kutta法求解,也可將獲得的常微分方程繼續用正交配置法離散為代數方程組。