數學模型
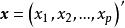 正交因子模型
正交因子模型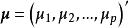 正交因子模型
正交因子模型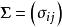 正交因子模型
正交因子模型設有p維可觀測的隨機向量 ,其均值為 ,協方差矩陣為 。因子分析的一般模型為
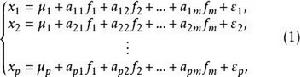 正交因子模型
正交因子模型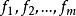 正交因子模型
正交因子模型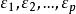 正交因子模型
正交因子模型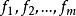 正交因子模型
正交因子模型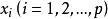 正交因子模型
正交因子模型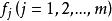 正交因子模型
正交因子模型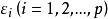 正交因子模型
正交因子模型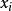 正交因子模型
正交因子模型其中 為公共因子, 為特殊因子,它們都是不可觀測的隨機變數。公共因子 出現在每一個原始變數 的表達式中,可理解為原始變數共同具有的公共因素;每個公共因子 一般至少對兩個原始變數有作用,否則可考慮將它歸人特殊因子。每個特殊因子 僅僅出現在與之相應的第i個原始變數 的表達式中,它只對這個原始變數有作用。(1)式可用矩陣、向量表示為
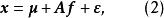 正交因子模型
正交因子模型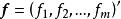 正交因子模型
正交因子模型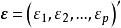 正交因子模型
正交因子模型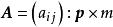 正交因子模型
正交因子模型式中 為公共因子向量, 為特殊因子向量, 稱為 因子載荷矩陣。通常假定
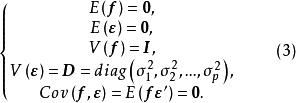 正交因子模型
正交因子模型該假定和關係式(2)構成了 正交因子模型。由上述假定可以看出,公共因子彼此不相關且具有單位方差,特殊因子也彼此不相關且和公共因子也不相關。
正交因子模型的性質
 正交因子模型
正交因子模型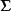 正交因子模型
正交因子模型1. 的協方差矩陣 的分解
由(2)、(3)知
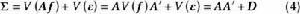 正交因子模型
正交因子模型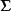 正交因子模型
正交因子模型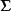 正交因子模型
正交因子模型這就是 的一個分解。如果 A只有少數幾列,則上述分解式揭示了 的一個簡單結構。由
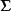 正交因子模型
正交因子模型於 D是對角矩陣,故 的非對角線元素可由 A的元素確定,即因子載荷完全決定了原始變數
 正交因子模型
正交因子模型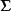 正交因子模型
正交因子模型之間的協方差。如果 為各分量已標準化了的隨機向量,則 就是相關矩陣 R,即有
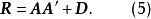 正交因子模型
正交因子模型 正交因子模型
正交因子模型 正交因子模型
正交因子模型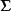 正交因子模型
正交因子模型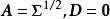 正交因子模型
正交因子模型分解式(4)是在 滿足正交因子模型的假定下推導出的,而對一般未作此假定的 ,(4)式是不容易準確得到的。當m=p時,任何協方差矩陣 均可按(4)式進行分解,如可取 ,但此時的分解對因子分析來說是毫無意義的,因為進行因子分析的目的就是要降維。在因子分析的大多數套用中,出於降維的需要,我們希望m要比p小得多,通常只能使這種分解近似成立,近似程度越好,表明因子模型擬合得越佳。
2.模型不受單位的影響
 正交因子模型
正交因子模型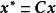 正交因子模型
正交因子模型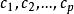 正交因子模型
正交因子模型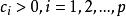 正交因子模型
正交因子模型將 的單位作變化,通常是作一變換 ,這裡 C=diag( ), ,於是
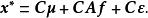 正交因子模型
正交因子模型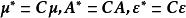 正交因子模型
正交因子模型令 ,則有
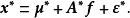 正交因子模型
正交因子模型這個模型能滿足完全類似於(3)式的假定,即
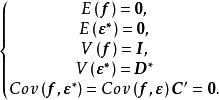 正交因子模型
正交因子模型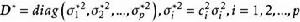 正交因子模型
正交因子模型其中 。因此,單位變換後新的模型仍為正交因子模型。
3.因子載荷是不唯一的
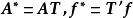 正交因子模型
正交因子模型設 T為任一m×m正交矩陣,令 ,則模型(2)能表示為
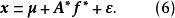 正交因子模型
正交因子模型因為
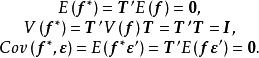 正交因子模型
正交因子模型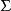 正交因子模型
正交因子模型所以仍滿足條件(3)。從(4)或(6)式都可看出, 也可分解為
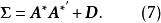 正交因子模型
正交因子模型顯然,因子載荷矩陣 A不是唯一的,在實際套用中常常利用這一-點,通過因子的旋轉使得新的因子有更好的實際意義。