概念
電路方面
電路微分方程的特徵根,稱為電路的固有頻率。當R(電阻)、L(電感)、C(電容)的量值不同時,特徵根可能出現以下三種情況,對應於三種不同的阻尼情況。
(1) R>2(L/C)^0.5時,S1、S2為不相等的實數根,為非振盪放電過程,為過阻尼情況。
(2) R=2(L/C)^0.5時,S1、S2為兩個相等的實數根,此時為臨界阻尼情況。
(3) R<2(L/C)^0.5時,S1、S2為共軛複數根,為振盪放電過程,為欠阻尼情況。
自動化領域
任何一個振動系統,當阻尼增加到一定程度時,物體的運動是非周期性的,物體振動連一次都不能完成,只是慢慢地回到平衡位置就停止了。一個系統受初擾動後不再受外界激勵,因受到阻力造成能量損失而位移峰值漸減的振動稱為阻尼振動。系統的狀態由阻尼率ζ來劃分。不同系統中ζ的計算式不同,但意義一樣。
(1) 當ζ=0時,系統無阻尼,即周期運動。
(2)當0<ζ<1時,系統所受的阻尼力較小,則要振動很多次,而振幅則在逐漸減小,最後才能達到平衡位置,這樣的運動叫欠阻尼狀態。
(3) 當ζ=1時,阻尼的大小剛好使系統作非“周期”運動,即阻力使振動物體剛能不作周期性振動而又能最快地回到平衡位置的情況,稱為“臨界阻尼”,或中肯阻尼狀態。
(4)當ζ>1時,阻尼再增大,系統需要很長時間才能達到平衡位置,這樣的運動叫過阻尼狀態。
與欠阻尼況和過阻尼相比,在臨界阻尼情況下,系統從運動趨近平衡所需的時間最短。
品質因數Q
品質因數Q是標誌欠阻尼振動系統的重要物理量之一,特別是在電磁振動(振盪)中它的意義更為突出。品質因數是為了描述振動系統在振動中能量耗散的情況而引人的。品質因數Q=儲能/耗能,定義為:
 欠阻尼
欠阻尼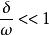 欠阻尼
欠阻尼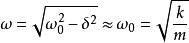 欠阻尼
欠阻尼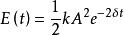 欠阻尼
欠阻尼 欠阻尼
欠阻尼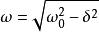 欠阻尼
欠阻尼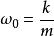 欠阻尼
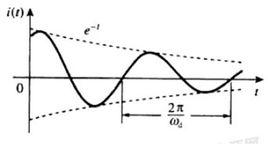
欠阻尼當阻尼很小時, ,又因為 ,所以, 。其中, 是阻尼因數,m是振子質量, 是振動的圓頻率, =k/m是振子固有圓頻率,k是彈性係數。
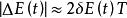 欠阻尼
欠阻尼當經歷的時間間隔△t恰為一個周期T時,因T很小,則系統在t至t+T的一個周期內所耗散的能量可以寫成 (式1)。
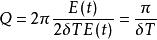 欠阻尼
欠阻尼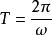 欠阻尼
欠阻尼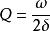 欠阻尼
欠阻尼 欠阻尼
欠阻尼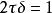 欠阻尼
欠阻尼 欠阻尼
欠阻尼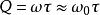 欠阻尼
欠阻尼根據定義 ,由於 ,則 。若引入弛豫時間 , ,由式(2)可以看出, 的物理意義是系統儲存的能量E耗散至E/e時所需要的時間。於是Q的表示式又可寫為 (式2)。
從式(2)可看出,Q就是在弛豫時間內,欠阻尼振動系統的相位變化量,它反映了此振盪系統的衰減特性。Q值越高,衰減越緩慢。
二階欠系統
定義
二階系統的標準數學模型如圖1所示。
 圖1
圖1開環傳遞函式為:
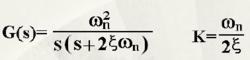 欠阻尼
欠阻尼閉環傳遞函式為(標準形式):
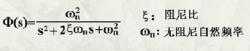 欠阻尼
欠阻尼它的特徵根為:
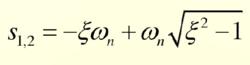 欠阻尼
欠阻尼當0<ζ<1時,系統欠阻尼。
階躍回響
二階欠阻尼系統的階躍回響為:
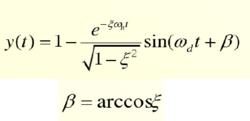 欠阻尼
欠阻尼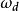 欠阻尼
欠阻尼其中,為有阻尼的自然振盪頻率。
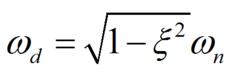 欠阻尼
欠阻尼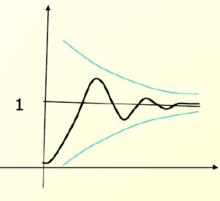 圖2 二階欠阻尼系統的回響曲線
圖2 二階欠阻尼系統的回響曲線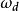 欠阻尼
欠阻尼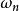 欠阻尼
欠阻尼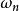 欠阻尼
欠阻尼在上述二階欠阻尼系統的階躍回響式中,第一項為單位階躍回響的穩態分量;第二項為動態分量,它是一以指數規律衰減的正弦振盪波,振盪頻率為,單位階躍回響y(t)衰減速度取決於共軛複數極點負實部ζ值大小,ζ(衰減係數)越大,共軛複數極點離虛軸越遠,y(t)衰減得越快。
上述二階欠阻尼系統對應的回響曲線如圖2所示。