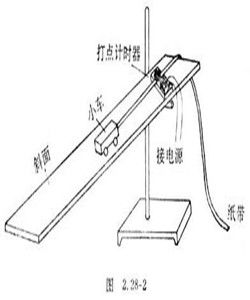
機械能守恆
機械能守恆物體的動能和勢能之和稱為物體的機械能，勢能可以是引力勢能，彈性勢能，庫倫勢等。例如：只有在重力（或彈簧的彈力）做功的情形下，物體的重力勢能（或彈性勢能）和動能發生相互轉化，但總機械能保持不變。
質點或質點系在勢力場(見保守系統)中運動時，其動能和勢能之和保持為常量。動能和勢能之和稱為機械能，故稱機械能守恆。機械能守恆的證明
設質點Q在勢力場中沿曲線Q1Q2運動(見圖)。有勢力F 沿曲線Q1Q2所作的功A12等於Q1、Q2兩點的勢能V1、V2的差，即A12＝V1-V2。 (1)
令v1和v2分別代表質點Q在Q1和Q2時的速度。由質點運動微分方程的切向投影式得：，
式中Ft為F沿曲線切向的分量。對上式兩邊乘以dS得：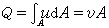
。
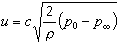， (2)
式中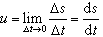
和 分別為質點Q在Q1和Q2點的動能。由此可見，質點在勢力場中運動時，機械能保持恆量。故勢力場又稱保守力場，有勢力又稱保守力。
質點在保守力場中運動時，沒有能量耗散，所以作用於質點的力所作的功只同質點的起始和終了的位置有關，而同質點運動的路徑無關。例如，質點沿路徑Q1Q2和Q1Q0Q2運動時，有勢力F 沿二路徑所作的功相等。
對於在有勢力場中的質點系，其機械能亦守恆，其勢能可用質心的勢能來計算。
守恆條件
只有重力或彈力做功，或系統的外力和非保守內力做功和為零。
表達式
機械能守恆重力勢能為與物體位置相關的能量，重力勢能具有相對性。表達式為Ep=mgh其中，m為質量，單位千克；g為重力常數，9.8N/kg；h為高度，物體相對於勢能參照面的高度(具有相對性，勢能參考面選擇不同，則h不同)，單位米。需要注意的是，h的數值具有相對性，但是對於一個運動過程來說，初始位置和最終位置的Δh是代數值，沒有相對性。
彈性勢能為(胡克定律的表達式為f=kx，其中k是勁度係數，x是物體的形變數。在國際單位制中，f的單位是牛，x的單位是米，它是形變數（彈性形變），k的單位是牛/米。勁度係數在數值上等於彈簧伸長（或縮短）單位長度時的彈力）
守恆方法
（1）做功條件分析法：
當發生動能與重力勢能的轉化時，只有重力做功，當發生動能與彈性勢能的轉化時，只有彈力做功，其他力均不做功，則系統的機械能守恆。
（2）能量轉換分析法：
若只有系統內物體間動能和重力勢能及彈性勢能的轉化，系統跟外界沒有發生機械能的傳遞，機械能也沒有轉化成其他形式的能（如沒有內能的增加，比如溫度升高），則系統的機械能守恆。
（3）增減情況分析法：
若系統的動能與勢能均增加或均減少，則系統的機械能不守恆：若系統的動能或勢能不變，而勢能或動能卻發生了變化，則系統的機械能不守恆：若系統內各個物體的機械能均增加或均減少，則系統的機械能也不守恆。
注意：在判斷機械能是否守恆時，一定要先選定系統（看清題目說定的系統）。
有兩種情況：
1.如果將產生彈力的的東西（比如說彈簧，下同）算作系統內的，那么機械能守恆。
2.如果將彈簧算作系統外的，那么機械能不守恆。此時彈簧的彈力對物體做功，使物體（系統）的動能和重力勢能有所改變。
例如，彈簧懸掛的小球。（高中物理練習中經常出錯的問題）
如果將小球和彈簧看成一個整體系統，則系統機械能是守恆的。
小球的機械能是不守恆。(平常大家說某物體的機械能，實質上是把物體與地球當做一個系統，是一種簡便說法。因為重力勢能是物體與地球所共有的。）
另外，對一些繩子突然繃緊、物體間碰撞等問題機械能一般不守恆，除非題目中有特別說明或暗示。
