名詞定義
modulus(複數形式為modulis)
材料在受力狀態下應力與應變之比。相應於不同的受力狀態,有不同的稱謂。例如,拉伸模量(E);剪下模量(G);體積模量(K);縱向壓縮量(L)等。該詞由拉丁語“小量度”演化而來。原來專指材料在彈性極限內的一個力學參數。故在不加任何定冠詞時往往就認為指彈性模量,即應力與應變之比是一常數。該值的大小是表示此材料在外力作用下抵抗彈性變形的能力。
彈性模量
拼音:tanxingmoliang
英文名稱: young's modulus/ elastic modulus/tensile modulus
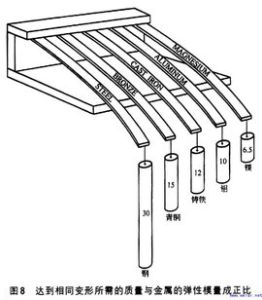
定義:材料在彈性變形階段,其應力和應變成正比例關係(即符合胡克定律-hooke's law),其比例係數稱為彈性模量。
單位:[力]/[長度]^2,在國際單位制中單位是Pa。
意義:彈性模量可視為衡量材料產生彈性變形難易程度的指標,其值越大,使材料發生一定彈性變形的應力也越大,即材料剛度越大,亦即在一定應力作用下,發生彈性變形越小。彈性模量E是指材料在外力作用下產生單位彈性變形所需要的應力。它是反映材料抵抗彈性變形能力的指標,相當於普通彈簧中的剛度。
彈性模量是彈性材料的一種最重要、最具特徵的力學性質。是物體彈性變形難易程度的表征。用E表示。定義為理想材料有小形變時應力與相應的應變之比。E以單位面積上承受的力表示,單位為牛/米^2。模量的性質依賴於形變的性質。剪下形變時的模量稱為剪下模量,用G表示;壓縮形變時的模量稱為壓縮模量,用K表示。模量的倒數稱為柔量,用J表示。
拉伸試驗中得到的屈服極限бb和強度極限бS,反映了材料對力的作用的承受能力,而延伸率δ或截面收縮率ψ,反映了材料縮性變形的能力,為了表示材料在彈性範圍內抵抗變形的難易程度,在實際工程結構中,材料彈性模量E的意義通常是以零件的剛度體現出來的,這是因為一旦零件按應力設計定型,在彈性變形範圍內的服役過程中,是以其所受負荷而產生的變形量來判斷其剛度的。一般按引起單位應變的負荷為該零件的剛度,例如,在拉壓構件中其剛度為:
式中A0為零件的橫截面積。
由上式可見,要想提高零件的剛度EA0,亦即要減少零件的彈性變形,可選用高彈性模量的材料和適當加大承載的橫截面積,剛度的重要性在於它決定了零件服役時穩定性,對細長桿件和薄壁構件尤為重要。因此,構件的理論分析和設計計算來說,彈性模量E是經常要用到的一個重要力學性能指標。
在彈性範圍內大多數材料服從虎克定律,即變形與受力成正比。拉伸彈性模量E,也叫楊氏模量。
彈性模量在比例極限內,材料所受應力如拉伸,壓縮,彎曲,扭曲,剪下等)與材料產生的相應應變之比,用牛/米^2表示。
動態模量
基本定義
由於應力導前應變一個相位角,使得應變分成了兩個部分,第一部分為彈性貢獻,與應變成線性關係,第二部分為粘性貢獻,與應變速率成線性關係。即彈性回響與粘性回響分別造成各自的應力,其線性加和就是材料的總應力。
相關公式
E(t)=|σ(t)|/|ε(t)|=σ/ε(1),式中E(t)為動態模量;σ(t)、ε(t)為應力和應變時間函式;σ、ε分別為應力和應變的振幅。由於相位差的存在,動態模量是一個複數,G=G’+iG’’,G’是彈性回響的係數,稱為儲能模量;G’’/ω為黏性回響的係數,故稱為損耗模量。G’和G’’合稱動態模量。