模擬測量與數字測量
正文
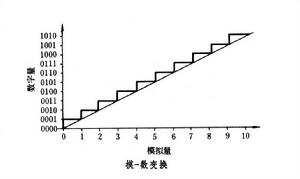
巨觀物理量本質上大都是固定或連續變化的模擬量。迄今為止的測量儀器的示值都模擬著被測量的變化。由於儀器本身的局限性，示值的分辨力只能達到2～3位有效數字，而且模擬式信號（測量數據）在測量過程中易受噪聲和干擾的影響而變值。隨著數位技術的發展，測量儀器日漸數位化。它使被測的模擬量通過模－數變換成為數字量，再利用數位技術和計算機成就來提高測量的精確度、可靠性、靈活性和自動化程度。數字式儀器用數碼顯示結果，讀數方便，不易讀錯，示值分辨力可達6、7位(電壓表)乃至 9、10位（頻率計數器）有效數字。而且數位訊號（測量數據）採用高－低兩個電平編碼信號，不易受干擾而出錯。數字量是離散量，以一定的跨步(量子值)躍變。每個數字量是一系列階躍跨步的總和,通常用n比特二進制編碼來表示。量化即模－數變換的結果（圖中粗線）只能在一些個別點全同於模擬量(細線)。二者之間不可避免的差異，稱為量化誤差或量化噪聲。二進編碼時,解析度(一個量子)為1/(2n-1)，8比特的解析度為±2×10-3,16比特的為±8×10-6,24比特的為±3×10-8。測量的動態範圍為n×6.02分貝。
模擬測量與數字測量
。顯然,τ應與被測之量v的變化速率(dv/dt)相適應。測量誤差為墹v=(墹v/墹t)τ。對於正弦變化量vsinωt，最大誤差將為墹v=vωτ或墹v/v=ωτ。把1千赫正弦信號量化到10比特,若要求墹v/v與數字解析度(1×10-3)相當，則要求τ≤160納秒。測量速度與精確度之間存在矛盾，精確度要求越高，則總採樣時間越長。 為了提高效率,可用較低的重複頻率fs<<1/τ來進行採樣，並在相繼二次採樣之間用保持電路來保持採得的值。若要從採樣結果復現原來的信號，根據採樣定理至少要求fs＞2fn，這裡fn是信號中所含的最高傅氏頻率分量，這樣復現的信號將無失真。然而，由於噪聲的影響,而且需要濾除採樣頻率fs,實際上要求fs＞5fn。採樣保持電路的作用猶如一個低通濾波器，其截頻為fs/2，並會產生一個相位延遲，其值為1/(2fs)。模-數變換在高速、高頻方面受到限制。
模-數變換的逆過程就是數-模變換，即從數字式編碼信號變換為對應的模擬式信號。當被變換的信號變化時，所得模擬信號呈現出量化階梯。用低通濾波器濾除階躍所產生的諧波，即得到平滑的模擬信號。若模擬信號中低頻傅氏分量的諧波低於高頻傅氏分量，則諧波的濾除顯然有困難。
除了可以用數-模變換電路作反饋來構成模-數變換器之外，在測量儀器和系統中,數-模變換器常用以產生模擬信號來驅動模擬式終端設備（例如X－Y繪圖儀和示波器等）和用於任意波形信號發生器。
