在通常的局面中，我們往往想通過少量的搜尋，為當前局面選擇一步較好的走法，然而在通常的棋局中，一個局面的評估往往不像輸、平、贏3種狀態這么簡單，在分不出輸贏的局面中棋局也有優劣之分。也就是說，要用更細緻的方法來刻畫局面的優劣，而不是僅僅使用1，-1,0三個數字刻畫3種終了局面。假定我們有一個函式可以為每一個局面的優劣評分。例如甲勝為正無窮，乙勝為負無窮，和局為0,；其他的情形依據雙方剩餘棋子的數量及位置評定從負無窮到正無窮之間的具體分數。這樣我們可以建立一棵固定深度的搜尋樹，其葉子節點不必是終了狀態，只是固定深度的最深一層的節點，其值由上述函式評出；對於中間節點，如同前面提到的那樣，甲方取子節點的最大值，乙方取子節點的最小值。這個評分的函式稱作靜態估值函式，用以取代固定深度的搜尋。顯然，我們無法擁有絕對精確的靜態估值函式，否則，只要這個靜態估值函式就可以解決所有的棋局了。估值函式給出的只是一個較粗略的評分，在此基礎上進行的少量搜尋的可靠性，理論上是不如前述的三種狀態的博弈樹的，但這種方法卻是可以實現的。利用具體的知識構成評估函式叫做啟發式搜尋。估值函式在有些文獻中也成為啟發式函式。
在博弈樹搜尋的文獻當中，極大極小方法往往指的是基於靜態估值函式的有限深度的極大極小搜尋。
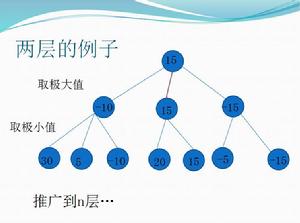極大極小值搜尋實例1.極大極小策略
是考慮雙方對弈若干步之後，從可能的步中選一步相對好的步法來走，即在有限的搜尋深度範圍內進行求解。
定義一個靜態估價函式f，以便對棋局的態勢做出優劣評估。
規定：
max和min代表對弈雙方；
p代表一個棋局（即一個狀態）；
有利於MAX的態勢，f(p)取正值；
有利於MIN的態勢，f(p)取負值；
態勢均衡，f(p)取零值；
在極大極小的搜尋當中，我們面臨著很多選擇，首先，是先在記憶體中生成整棵樹然後進行搜尋，還是在搜尋的過程中僅僅產生將要搜尋的節點？其次，對於樹的搜尋是以什麼順序進行，是廣度優先還是深度優先還是其他？最後，有必要生成整棵樹嗎，在搜尋過程中需要將搜尋過的節點刪去嗎？在計算機能力有限的情況下，要使搜尋引擎搜尋更深並且判斷局面的好壞是相當耗時間的，這就需要極大極小搜尋的剪枝。
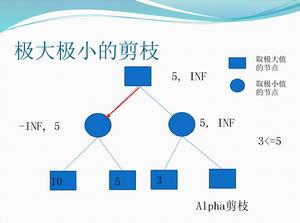Alpha剪枝
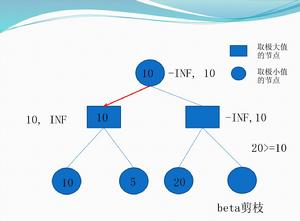Beta剪枝