定義
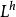 極大積分流形
極大積分流形 極大積分流形
極大積分流形 極大積分流形
極大積分流形 極大積分流形
極大積分流形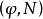 極大積分流形
極大積分流形 極大積分流形
極大積分流形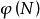 極大積分流形
極大積分流形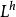 極大積分流形
極大積分流形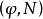 極大積分流形
極大積分流形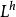 極大積分流形
極大積分流形設是定義在維光滑流形上的維光滑分布,設是分布的一個連通的積分流形,並且它的象不是的另一個連通積分流形的真子集,則稱是的 極大積分流形 。
相關定理
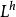 極大積分流形
極大積分流形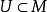 極大積分流形
極大積分流形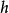 極大積分流形
極大積分流形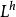 極大積分流形
極大積分流形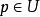 極大積分流形
極大積分流形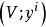 極大積分流形
極大積分流形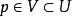 極大積分流形
極大積分流形定理1 (Frobenius定理) 設是定義在開子集上的維光滑分布,如果滿足Frobenius條件,則在每一點,存在局部坐標系,使得,並且
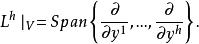 極大積分流形
極大積分流形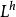 極大積分流形
極大積分流形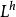 極大積分流形
極大積分流形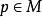 極大積分流形
極大積分流形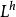 極大積分流形
極大積分流形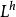 極大積分流形
極大積分流形定理2 設M是具有第二可數公理的m維光滑流形,是M上的h維光滑分布,如果滿足Frobenius條件,則對於任意一點,必存在的唯一的一個極大積分流形經過點p,並且的經過點p的每一個連通積分流形必包含在這個極大積分流形內 。
下面敘述關於定理證明的大意。
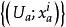 極大積分流形
極大積分流形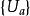 極大積分流形
極大積分流形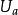 極大積分流形
極大積分流形根據Frobenius定理,在M上存在一族局部坐標系,其中構成M的可數開覆蓋,且在中的坐標面
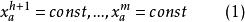 極大積分流形
極大積分流形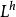 極大積分流形
極大積分流形是的h維積分流形。
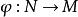 極大積分流形
極大積分流形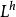 極大積分流形
極大積分流形設N是連通的h維光滑流形,且是的積分流形,即
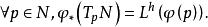 極大積分流形
極大積分流形 極大積分流形
極大積分流形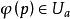 極大積分流形
極大積分流形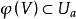 極大積分流形
極大積分流形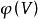 極大積分流形
極大積分流形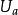 極大積分流形
極大積分流形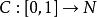 極大積分流形
極大積分流形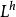 極大積分流形
極大積分流形根據的連續性,若,則有點p在N中的連通鄰域V,使得,故包含在的某個坐標面(1)內,設q是N上另外一點,C是聯結p,q的分段光滑曲線,則C可以用有限多個如上所述的鄰域V覆蓋住。換句話說,N上任意一點q都能用分段光滑曲線與點p連結起來,並且其中每一段光滑曲線都是的一維積分流形,即有[0,1]的分割
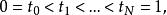 極大積分流形
極大積分流形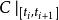 極大積分流形
極大積分流形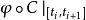 極大積分流形
極大積分流形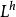 極大積分流形
極大積分流形使得每一段曲線是光滑的,並且是的一維積分流形。
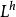 極大積分流形
極大積分流形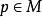 極大積分流形
極大積分流形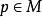 極大積分流形
極大積分流形上述討論啟發我們如何去構造分布的經過點的極大積分流形。設,令
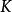 極大積分流形
極大積分流形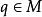 極大積分流形
極大積分流形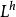 極大積分流形
極大積分流形={:q能用分段光滑曲線與p連結,且每段光滑曲線是的一維積分流形). (2)
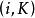 極大積分流形
極大積分流形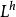 極大積分流形
極大積分流形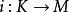 極大積分流形
極大積分流形在K上能引進光滑流形結構,使之成為h維連通光滑流形,並可證明是的經過點p的極大積分流形,這裡是包含映射。
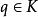 極大積分流形
極大積分流形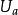 極大積分流形
極大積分流形事實上,若,則q必屬於某個,於是坐標面
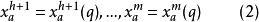 極大積分流形
極大積分流形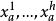 極大積分流形
極大積分流形的含有q的連通分支必包含在K內,將該連通分支取為點q在K中的坐標鄰域,且以
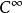 極大積分流形
極大積分流形為其中的局部坐標。可以驗證,這樣給出的坐標鄰域構成K的-坐標覆蓋,從而使K成為h
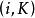 極大積分流形
極大積分流形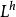 極大積分流形
極大積分流形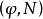 極大積分流形
極大積分流形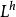 極大積分流形
極大積分流形維光滑流形,且是的積分流形。根據K的定義以及前面的討論,若是的經過
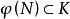 極大積分流形
極大積分流形點p的連通積分流形,則必有,因此K是極大的。
由定理2可見,在M中存在一族h維連通的、單一浸入的子流形,滿足如下條件:
(1)對於M上任意一點p,必有族中的一個子流形通過它;
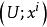 極大積分流形
極大積分流形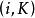 極大積分流形
極大積分流形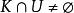 極大積分流形
極大積分流形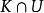 極大積分流形
極大積分流形(2)存在點p的局部坐標系,使得在族中的子流形滿足時,的連通分支為
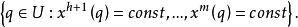 極大積分流形
極大積分流形這樣的子流形族稱為M的一個 葉狀結構(foliation),其中的每一個子流形稱為 葉(leaf),因此,定理2的意義是:M上滿足Frobenius條件的h維分布在M上決定了一個葉狀結構。關於葉狀結構的拓撲和幾何的研究,是60年代以來一個重要的課題 。

