定義
 極大理想
極大理想設N是環R的一個理想,且,如果除R和N外,R中沒有包含N的其他理想,則稱N為環R的一個 極大理想。
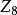 極大理想
極大理想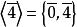 極大理想
極大理想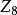 極大理想
極大理想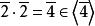 極大理想
極大理想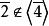 極大理想
極大理想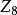 極大理想
極大理想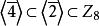 極大理想
極大理想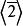 極大理想
極大理想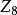 極大理想
極大理想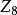 極大理想
極大理想例1 在模8剩餘類環中,理想不是的素理想(因為,但是),也不是的極大理想(因為)。但是,易知理想既是的素理想也是的極大理想。
應該注意的是,素理想是在交換環內定義的,但極大理想並無這種限制。
定理
定理1
設N是整數環Z的一個理想,則
 極大理想
極大理想 極大理想
極大理想 極大理想
極大理想是極大理想由素數生成.
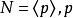 極大理想
極大理想證明 設是素數,又K是Z的一個理想,且
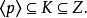 極大理想
極大理想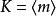 極大理想
極大理想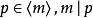 極大理想
極大理想 極大理想
極大理想令,則,只有或p,即只有
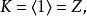 極大理想
極大理想或
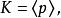 極大理想
極大理想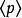 極大理想
極大理想從而是Z的極大理想。
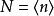 極大理想
極大理想反之,設N是Z的極大理想,由於Z的理想都是主理想,故可設,且不妨設n是正整數,如果n是合數,令
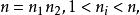 極大理想
極大理想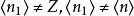 極大理想
極大理想則Z的理想,但卻有
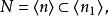 極大理想
極大理想這與N是Z的極大理想矛盾.故n必為素數。(證畢)。
根據這個定理,並由例1可知,除平凡理想外,整數環的素理想和極大理想是一致的,但是,對有些環來說並不是這樣。
定理2
設N是環R的一個理想,則
 極大理想
極大理想 極大理想
極大理想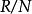 極大理想
極大理想是極大理想今是單環.
 極大理想
極大理想證明 用表示R到R=R/N的自然同態。
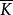 極大理想
極大理想 極大理想
極大理想 極大理想
極大理想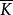 極大理想
極大理想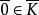 極大理想
極大理想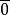 極大理想
極大理想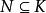 極大理想
極大理想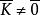 極大理想
極大理想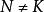 極大理想
極大理想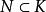 極大理想
極大理想設N是R的一個極大理想,而為的任一非零理想,則由相應定理知,在之下的逆像K是R的一個理想。由於,而的逆像為N,故,又因,故,即,但N是R的極大理想,故
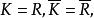 極大理想
極大理想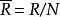 極大理想
極大理想即只有平凡理想,R/N是單環。
 極大理想
極大理想反之,設是單環,K是R的一個理想,且
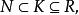 極大理想
極大理想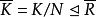 極大理想
極大理想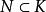 極大理想
極大理想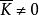 極大理想
極大理想 極大理想
極大理想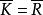 極大理想
極大理想則.但由於,故,又因是單環,故。
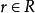 極大理想
極大理想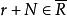 極大理想
極大理想 極大理想
極大理想任取,則,從而有使
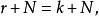 極大理想
極大理想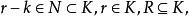 極大理想
極大理想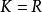 極大理想
極大理想於是因此,即N是R的極大理想。(證畢)。
我們知道,域是單環,以下將指出,在一定條件下其逆也成立。
定理3
設環R是一個單環,則當R有單位元且可換時,R是一個域。
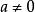 極大理想
極大理想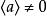 極大理想
極大理想證明 在R中任取,則.但R是單環,只有平凡理想,故
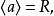 極大理想
極大理想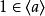 極大理想
極大理想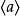 極大理想
極大理想於是單位元,但對有單位元的交換環來說,中元素都可表為
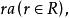 極大理想
極大理想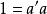 極大理想
極大理想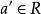 極大理想
極大理想於是,其中,即R中每個非零元都有逆元,從而R是一個域。(證畢)。
由以上兩個定理立即可得下面推論。
推論1
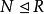 極大理想
極大理想設R是一個有單位元的交換環,,則
 極大理想
極大理想 極大理想
極大理想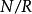 極大理想
極大理想是極大理想是域.
證明 設R/N是域,而域是單環,於是由定理2知,N是R的一個極大理想。
反之,設N是R的一個極大理想,由定理2,R/N是單環,又因環R有單位元且可換,從而R/N也有單位元且可換,故由定理3,R/N是一個域。(證畢)。
根據這個推論,再結合定理1又可得下面推論。
推論2
有單位元的交換環的極大理想必為素理想。
這樣,在有單位元的交換環中,只要給出一個極大理想,便可立即得到一個與這個環有密切聯繫的域,於是,可以通過所得到的域進一步研究所給的環。
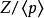 極大理想
極大理想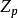 極大理想
極大理想例2 由素數p生成的理想是整數環Z的極大理想,而Z有單位元且可換,故由推論1知,即是一個域。
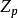 極大理想
極大理想這樣,我們從極大理想出發,又一次證明了是一個域。

