定義
假定:輸入是由一個隨機過程產生的[0, 1)區間上均勻分布的實數。將區間[0, 1)劃分為n個大小相等的子區間(桶),每桶大小1/n:[0, 1/n), [1/n, 2/n), [2/n, 3/n),…,[k/n, (k+1)/n ),…將n個輸入元素分配到這些桶中,對桶中元素進行排序,然後依次連線桶輸入0 ≤A[1..n] <1輔助數組B[0..n-1]是一指針數組,指向桶(鍊表)。
算法思想
平均情況下桶排序以線性時間運行。像計數排序一樣,桶排序也對輸入作了某種假設, 因而運行得很快。具體來說,計數排序假設輸入是由一個小範圍內的整數構成,而桶排序則 假設輸入由一個隨機過程產生,該過程將元素一致地分布在區間[0,1)上。
桶排序的思想就是把區間[0,1)劃分成n個相同大小的子區間,或稱桶,然後將n個輸入數分布到各個桶中去。因為輸入數均勻分布在[0,1)上,所以一般不會有很多數落在 一個桶中的情況。為得到結果,先對各個桶中的數進行排序,然後按次序把各桶中的元素列 出來即可。
在桶排序算法的代碼中,假設輸入是個含n個元素的數組A,且每個元素滿足0≤ A[i]<1。另外還需要一個輔助數組B[O..n-1]來存放鍊表實現的桶,並假設可以用某種機制來維護這些表。
桶排序的算法如下(偽代碼表示),其中floor(x)是地板函式,表示不超過x的最大整數。
procedure Bin_Sort(var A:List);
 桶排序算法
桶排序算法n:=length(A);
for i:=1 to n do
將A[i]插到表B[floor(n*A[i])]中;
for i:=0 to n-1 do
用插入排序對表B[i]進行排序;
將表B[0],B[1],...,B[n-1]按順序合併;
end;
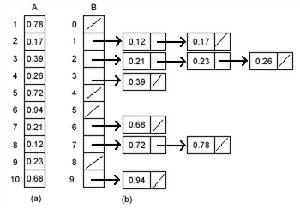
右圖演示了桶排序作用於有10個數的輸入數組上的操作過程。(a)輸入數組A[1..10]。(b)在該算法的第5行後的有序表(桶)數組B[0..9]。桶i中存放了區間[i/10,(i+1)/10]上的值。排序輸出由表B[O]、B[1]、...、B[9]的按序並置構成。
要說明這個算法能正確地工作,看兩個元素A[i]和A[j]。如果它們落在同一個桶中,則它們在輸出序列中有著正確的相對次序,因為它們所在的桶是採用插入排序的。現假設它們落到不同的桶中,設分別為B[i']和B[j']。不失一般性,假設i' i'=floor(n*A[i])≥floor(n*A[j])=j' 得矛盾 (因為i' 現在來分析算法的運行時間。除第5行外,所有各行在最壞情況的時間都是O(n)。第5行中檢查所有桶的時間是O(n)。分析中唯一有趣的部分就在於第5行中插人排序所花的時間。
為分析插人排序的時間代價,設ni為表示桶B[i]中元素個數的隨機變數。因為插入排序以二次時間運行,故為排序桶B[i]中元素的期望時間為E[O(ni2)]=O(E[ni2]),對各個桶中的所有元素排序的總期望時間為:O(n)。

(2)將這個界用到(1)式上,得出桶排序中的插人排序的期望運行時間為O(n)。因而,整個桶排序的期望運行時間就是線性的。
時間空間代價分析
桶排序利用函式的映射關係,減少了幾乎所有的比較工作。實際上,桶排序的f(k)值的計算,其作用就相當於快排中劃分,已經把大量數據分割成了基本有序的數據塊(桶)。然後只需要對桶中的少量數據做先進的比較排序即可。
對N個關鍵字進行桶排序的時間複雜度分為兩個部分:
(1) 循環計算每個關鍵字的桶映射函式,這個時間複雜度是O(N)。
(2) 利用先進的比較排序算法對每個桶內的所有數據進行排序,其時間複雜度為 ∑ O(Ni*logNi) 。其中Ni 為第i個桶的數據量。
很顯然,第(2)部分是桶排序性能好壞的決定因素。儘量減少桶內數據的數量是提高效率的唯一辦法(因為基於比較排序的最好平均時間複雜度只能達到O(N*logN)了)。因此,我們需要儘量做到下面兩點:
(1) 映射函式f(k)能夠將N個數據平均的分配到M個桶中,這樣每個桶就有[N/M]個數據量。
(2) 儘量的增大桶的數量。極限情況下每個桶只能得到一個數據,這樣就完全避開了桶內數據的“比較”排序操作。 當然,做到這一點很不容易,數據量巨大的情況下,f(k)函式會使得桶集合的數量巨大,空間浪費嚴重。這就是一個時間代價和空間代價的權衡問題了。
對於N個待排數據,M個桶,平均每個桶[N/M]個數據的桶排序平均時間複雜度為:
O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM)
當N=M時,即極限情況下每個桶只有一個數據時。桶排序的最好效率能夠達到O(N)。
總結: 桶排序的平均時間複雜度為線性的O(N+C),其中C=N*(logN-logM)。如果相對於同樣的N,桶數量M越大,其效率越高,最好的時間複雜度達到O(N)。當然桶排序的空間複雜度為O(N+M),如果輸入數據非常龐大,而桶的數量也非常多,則空間代價無疑是昂貴的。此外,桶排序是穩定的。
AAuto語言實現桶排序
io.open();//打開控制台
/**-------------------------------------------------------* 桶排序**------------------------------------------------------*/
/*
桶排序假設輸入元素均勻而獨立分布在區間[0,1) 即 0 <= x and x < 1;將區間劃分成n個相同大小的子區間(桶),然後將n個輸入按大小分布到各個桶中去,對每個桶內部進行排序。最後將所有桶的排序結果合併起來.
*/
//插入排序算法
insert_sort = function( array ){
for( right=2;#array ) {
var top = array[right];
//Insert array[right] into the sorted seqquence array[1....right-1]
var left = right -1;
while( left and array[left]>top){
array[left+1] = array[left];
left--;
}
array[left+1] = top;
}
return array;
}
//桶排序算法
bucket_sort = function( array ){
var n = #array;
var bucket ={}
for(i=0;n;1){
bucket[i] = {} //創建一個桶
}
var bucket_index
for(i=1;n;1){
bucket_index = math.floor(n * array[i]);
table.push( bucket [ bucket_index ],array[i] );//放到桶里去
}
for(i=1;n;1){
insert_sort( bucket[i] ); //對每個桶進行插入排序
}
return table.concat( table.unpack(bucket) )
}
io.print("----------------")
io.print("桶排序")
io.print("----------------")
array={};
//桶排序假設輸入是由一個隨機過程產生的小數.
math.randomize()
for(i=1;20;1){
table.push( array,math.random() )
}
//排序
array = bucket_sort( array )
//輸出結果
for(i=1;#array;1){
io.print( array[i] )
}
execute("pause") //按任意鍵繼續
io.close();//關閉控制台
C++實現源碼
#include<iostream>
using namespace std;
int a[]={1,255,8,6,25,47,14,35,58,75,96,158,657};
const int len=sizeof(a)/sizeof(int);
int b[9][len]={0};//將b全部置0
void bucketSort(int a[]); //桶排序函式
void distributeElments(int a[],int b[9][len],int digits);
void collectElments(int a[], int b[9][len]);
int numOfDigits(int a[]);
void zeroBucket(int b[9][len]); //將b數組中的全部元素置0
int main()
{
cout<<"原始數組:";
for(int i=0; i<len; i++)
cout<<a[i]<<",";
cout<<endl;
bucketSort(a);
cout<<"排序後數組:";
for(int i=0; i<len; i++)
cout<<a[i]<<",";
cout<<endl;
return 0;
}
void bucketSort(int a[])
{
int digits=numOfDigits(a);
for(int i=1; i<=digits; i++)
{
distributeElments(a,b,i);
collectElments(a,b);
if(i!=digits)
zeroBucket(b);
}
}
int numOfDigits(int a[])
{
int largest=0;
for(int i=0; i<len; i++) //獲取最大值
if(a[i]>largest)
largest=a[i];
int digits=0; //digits為最大值的位數
while(largest)
{
digits++;
largest/=10;
}
return digits;
}
void distributeElments(int a[],int b[9][len],int digits)
{
int divisor=10; //除數
for(int i=1; i<digits; i++)
divisor*=10;
for(int j=0; j<len; j++)
{
int numOfDigist=(a[j]%divisor-a[j]%(divisor/10))/(divisor/10);
//numOfDigits為相應的(divisor/10)位的值,如當divisor=10時,求的是個位數
int num = ++b[numOfDigist][0];//用b中第一列的元素來儲存每行中元素的個數
b[numOfDigist][num]=a[j];
}
}
void collectElments(int a[], int b[9][len])
{
int k=0;
for(int i=0; i<=9; i++)
for(int j=1; j<=b[i][0]; j++)
a[k++]=b[i][j];
}
void zeroBucket(int b[][len])
{
for(int i=0; i<9; i++)
for(int j=0; j<len; j++)
b[i][j]=0;
}
JAVA實現源碼
public static void basket(int data[]) //data為待排序數組
{
int n = data.length;
int bask[][] = new int[10][n];
int index[] = new int[10];
int max = Integer.MIN_VALUE;
for(int i = 0; i < n; i++)
{
max = max > (Integer.toString(data[i]).length()) ? max : (Integer.toString(data[i]).length());
}
String str;
for(int i = max - 1; i >= 0; i--)
{
for(int j = 0; j < n; j++)
{
str = "";
if(Integer.toString(data[j]).length() < max)
{
for(int k = 0; k < max - Integer.toString(data[j]).length(); k++)
str += "0";
}
str += Integer.toString(data[j]);
bask[str.charAt(i)-'0'][index[str.charAt(i)-'0']++] = data[j];
}
int pos = 0;
for(int j = 0; j < 10; j++)
{
for(int k = 0; k < index[j]; k++)
{
data[pos++] = bask[j][k];
}
}
for(int x = 0; x < 10; x++)index[x] = 0;
}
}
桶排序的套用
海量數據中的套用一年的全國聯考考生人數為500 萬,分數使用標準分,最低100 ,最高900 ,沒有小數,你把這500 萬元素的數組排個序。
分析:對500W數據排序,如果基於比較的先進排序,平均比較次數為O(5000000*log5000000)≈1.112億。但是我們發現,這些數據都有特殊的條件: 100=<score<=900。那么我們就可以考慮桶排序這樣一個“投機取巧”的辦法、讓其在毫秒級別就完成500萬排序。
方法:創建801(900-100)個桶。將每個考生的分數丟進f(score)=score-100的桶中。這個過程從頭到尾遍歷一遍數據只需要500W次。然後根據桶號大小依次將桶中數值輸出,即可以得到一個有序的序列。而且可以很容易的得到100分有***人,501分有***人。
實際上,桶排序對數據的條件有特殊要求,如果上面的分數不是從100-900,而是從0-2億,那么分配2億個桶顯然是不可能的。所以桶排序有其局限性,適合元素值集合併不大的情況。
在一個檔案中有10G個整數,亂序排列,要求找出中位數。記憶體限制為2G。只寫出思路即可(記憶體限制為2G意思是可以使用2G空間來運行程式,而不考慮本機上其他軟體記憶體占用情況。) 關於中位數:數據排序後,位置在最中間的數值。即將數據分成兩部分,一部分大於該數值,一部分小於該數值。中位數的位置:當樣本數為奇數時,中位數=(N+1)/2 ; 當樣本數為偶數時,中位數為N/2與1+N/2的均值(那么10G個數的中位數,就第5G大的數與第5G+1大的數的均值了)。
分析:既然要找中位數,很簡單就是排序的想法。那么基於位元組的桶排序是一個可行的方法。
思想:將整型的每1byte作為一個關鍵字,也就是說一個整形可以拆成4個keys,而且最高位的keys越大,整數越大。如果高位keys相同,則比較次高位的keys。整個比較過程類似於字元串的字典序。
第一步:把10G整數每2G讀入一次記憶體,然後一次遍歷這536,870,912即(1024*1024*1024)*2 /4個數據。每個數據用位運算">>"取出最高8位(31-24)。這8bits(0-255)最多表示255個桶,那么可以根據8bit的值來確定丟入第幾個桶。最後把每個桶寫入一個磁碟檔案中,同時在記憶體中統計每個桶內數據的數量,自然這個數量只需要255個整形空間即可。
代價:(1) 10G數據依次讀入記憶體的IO代價(這個是無法避免的,CPU不能直接在磁碟上運算)。(2)在記憶體中遍歷536,870,912個數據,這是一個O(n)的線性時間複雜度。(3)把255個桶寫會到255個磁碟檔案空間中,這個代價是額外的,也就是多付出一倍的10G數據轉移的時間。
第三步:繼續以記憶體中的整數的次高8bit進行桶排序(23-16)。過程和第一步相同,也是255個桶。
第四步:一直下去,直到最低位元組(7-0bit)的桶排序結束。我相信這個時候完全可以在記憶體中使用一次快排就可以了。
代價:(1)循環計算255個桶中的數據量累加,需要O(M)的代價,其中m<255。(2)讀入一個大概80M左右檔案大小的IO代價。
注意,變態的情況下,這個需要讀入的第128號檔案仍然大於2G,那么整個讀入仍然可以按照第一步分批來進行讀取。第二步:根據記憶體中255個桶內的數量,計算中位數在第幾個桶中。很顯然,2,684,354,560個數中位數是第1,342,177,280個。假設前127個桶的數據量相加,發現少於1,342,177,280,把第128個桶數據量加上,大於1,342,177,280。說明,中位數必在磁碟的第128個桶中。而且在這個桶的第1,342,177,280-N(0-127)個數位上。N(0-127)表示前127個桶的數據量之和。然後把第128個檔案中的整數讀入記憶體。(平均而言,每個檔案的大小估計在10G/128=80M左右,當然也不一定,但是超過2G的可能性很小)。
整個過程的時間複雜度在O(n)的線性級別上(沒有任何循環嵌套)。但主要時間消耗在第一步的第二次記憶體-磁碟數據交換上,即10G數據分255個檔案寫回磁碟上。一般而言,如果第二步過後,記憶體可以容納下存在中位數的某一個檔案的話,直接快排就可以了。
