格子方

在數學中，格子方是二維歐幾里德空間中的一種晶格。它是整數晶格的二維形式，表示為Z。它是按照它們的對稱群分類的五種二維格子之一 。直立方形和對角線方形是迄今為止最常見的，它們可以方便地稱為直立方格和對角方格; 後者也稱為中心正方形格子。

簡介

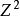格子方

格子方是二維歐幾里德空間中的一種晶格。它是整數晶格的二維形式，表示為 。直立方形格子（圖1左邊）和對角線方形格子（圖1右邊）是迄今為止最常見的兩種格子方，它們可以方便地稱為直立方格和對角方格;後者也稱為 中心正方形格子。兩者相差45°角，這與正方形格子可以被分割成兩個方格子格的事實相關，這在棋盤格的著色中很明顯 。

圖1.方格子（左邊為直立方形格子，右邊為對角線方形格子）

對稱性

格子方

正方形格子的對稱類別是圖p4m，具有這種平移對稱晶格的圖案有很多，但可能具有比晶格本身更少的對稱性。直立正方形格子可以看作是，對角正方形格子 倍放大大，且增加了正方形的中心。相應地，在添加直立正方形格子的正方形中心之後，我們有一個對角正方形格子，其格線尺寸是原始格子的尺寸的2倍，是具有4倍旋轉中心的正方形晶格。

關於反射軸有三種可能性 ：

（1）沒有反射軸，如圖2；

（2）在四個方向均有反射軸，如圖4；

（3）在兩個垂直方向上有反射軸，如圖3。

反射軸的交點形成一個正方形格線，與四重旋轉中心的正方形格線一樣好，並且方向相同，這些旋轉中心位於由反射軸形成的正方形的中心。

圖1.p4，[4,4] +，（442）

圖2.p4g，[4,4 + ]，（4 * 2）

圖3.p4m，[4,4]，（* 442）

圖2為p4，其排列在2和4倍旋轉中心的晶格內（也適用於p4g和p4m），一個基本域用黃色表示。

圖3為p4g，其在兩個方向上有反射軸，而不是通過4倍旋轉中心。

格子方

圖4為p4m，其在四個方向上有反射軸，通過四重旋轉中心。在兩個方向上，反射軸的方向與p4g的方向相同且密度相同，但偏移。在另外兩個方向上，它們是線性的 密度因子。