根軸方程
設兩圓O1,O2的方程分別為:
(x-a1)^2+(y-b1)^2-(r1)^2=0(1)
(x-a2)^2+(y-b2)^2-(r2)^2=0(2)
由於根軸上任意點對兩圓的圓冪相等,所以根軸上任一點(x,y),有
(x-a1)^2+(y-b1)^2-(r1)^2=圓冪=(x-a2)^2+(y-b2)^2-(r2)^2
兩式相減,得根軸的方程(即x,y的方程)為
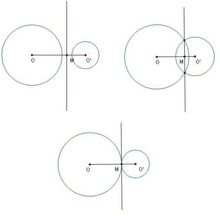 根軸
根軸2(a2-a1)x+2(b2-b1)y+f1-f2=0
其中f1=(a1)^2+(b1)^2-(r1)^2,f2類似。
相關定理
1,平面上任意兩圓的根軸垂直於它們的連心線;
2,若兩圓相交,則兩圓的根軸為公共弦所在的直線;
3,若兩圓相切,則兩圓的根軸為它們的內公切線;
4,若兩圓外離,則兩圓的根軸上的點分別引兩圓的切線,則切線長相等。從而,根軸必過四條公切線的中點。
5,蒙日定理(根心定理):平面上任意三個圓,若這三個圓圓心不共線,則三條根軸相交於一點,這個點叫它們的根心;若三圓圓心共線,則三條根軸互相平行;
6,反演後的圓和反演圓和被反演的圓3個圓共根軸。