柯西型積分
 柯西核
柯西核柯西型積分是柯西積分的推廣。下列積分稱為柯西型積分: 其中L為封閉的或開口的可求長曲線。
柯西核定義
 柯西核
柯西核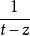 柯西核
柯西核在柯西型積分的表達式 中,f(t)稱為它的核密度, 稱為柯西核。
柯西核的奇異積分方程
柯西核的奇異積分方程包括希爾伯特核的奇異積分方程,這是研究得最早和最完整的一類方程。
柯西核的奇異積分方程的特點是未知函式出現在發散的積分號下,該積分只在柯西主值下有意義,以及和它的特徵方程有密切聯繫的黎曼問題。
在柯西型積分的表達式中,f(t)稱為它的核密度,1/t-z稱為柯西核。柯西核的奇異積分方程包括希爾伯特核的奇異積分方程,這是研究得最早和最完整的一類方程。
 柯西核
柯西核柯西型積分是柯西積分的推廣。下列積分稱為柯西型積分: 其中L為封閉的或開口的可求長曲線。
 柯西核
柯西核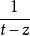 柯西核
柯西核在柯西型積分的表達式 中,f(t)稱為它的核密度, 稱為柯西核。
柯西核的奇異積分方程包括希爾伯特核的奇異積分方程,這是研究得最早和最完整的一類方程。
柯西核的奇異積分方程的特點是未知函式出現在發散的積分號下,該積分只在柯西主值下有意義,以及和它的特徵方程有密切聯繫的黎曼問題。
柯西奇異積分方程(Cauehy singular integral equations)是一類最基本且具有廣泛實際套用的奇異積分方程,其積分是柯西主值意...
定義 分類 特徵方程與相聯方程 性質 重要定理柯西-賽格積分表示是單複變函數論中柯西型積分的推廣。華羅庚引進並證明了在一般有界圓型星形域上,存在一類柯西積分公式,稱為柯西-賽格積分公式。
推導 柯西-賽格核 辨析廣義柯西公式,亦稱廣義柯西型積分,是解析函式柯西公式的推廣。
簡介 推導 基本核條件 解析函式爛柯山又名石室山、石橋山,位於衢州城東南13公處,面臨烏溪江,與全國重點大型化工企業浙江巨化集團隔江相望。爛柯山黛峰翠嶂,景極幽邃。爛柯山腳赭紅色的圍牆...
基本簡介 遊覽勝地 景區簡介 名稱由來 城市交通棗核治走馬牙疳:陳年南棗核,,嬈灰研求摻之。(王坫桂《不藥良方》)治跟疾紅線鎖目:取南棗核二十一粒,將核截兩端去仁淨,以銅綠塞孔中,仍將棗核合上,以紙封...
中藥材 散文 作者資料 關於文章柯瑾(1715-1786)派名增修,字淳倩,號禺峰,湖北省大冶市陳貴鎮石堰柯莊人,生於清康熙己未(1715年)古歷七月十三日子時。早年入武昌府廩生,先後...
人物簡介 為官簡歷 屢膺御賜 柯瑾軼事 柯瑾拜壽柯伊伯帶是太陽系在海王星軌道(距離太陽約30天文單位)外黃道面附近、天體密集的中空圓盤狀區域。柯伊伯帶的假說最初是由愛爾蘭裔天文學家艾吉沃斯提出,傑拉德...
起源 詳解 命名 組織 研究爛柯山,又名石室山、石橋山,位於浙江省衢州市東南10公里處,與全國重點大型化工企業衢州化學工業公司隔江相望。此山黛峰翠嶂,景極幽邃。是浙江省重點名勝風景...
基本簡介 遊覽勝地 景區簡介 名稱由來 城市交通米粒影業作品,科幻機甲真人特效電影,是國產首部機甲太空大片。
簡介 電影劇情 主創信息 電影《星核》一部國人開“天”之作 專訪|《三體》之後看《星核》