定義
柯西奇異積分方程是一類最基本且具有廣泛實際套用的奇異積分方程。
下面的一類積分方程
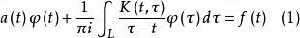 柯西奇異積分方程
柯西奇異積分方程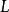 柯西奇異積分方程
柯西奇異積分方程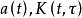 柯西奇異積分方程
柯西奇異積分方程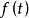 柯西奇異積分方程
柯西奇異積分方程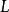 柯西奇異積分方程
柯西奇異積分方程稱為 柯西奇異積分方程。其中 為複平面上一光滑的閉合曲線, 和 是給定在 上滿足赫爾德條件的函式,而積分是柯西主值意義下的。
分類
柯西奇異積分方程的研究已有很長的歷史,差不多在建立弗雷德霍姆理論的同時,即已出現在希爾伯特和龐加萊等人的工作中,以後經過許多數學家的努力,這一類方程的理論已發展得相當完善。它在彈性理論、空氣動力學、水力學、量子場論以及數學物理等方面有著廣泛的套用。若記
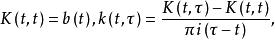 柯西奇異積分方程
柯西奇異積分方程則柯西奇異積分方程(1)可寫成
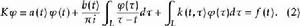 柯西奇異積分方程
柯西奇異積分方程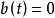 柯西奇異積分方程
柯西奇異積分方程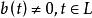 柯西奇異積分方程
柯西奇異積分方程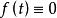 柯西奇異積分方程
柯西奇異積分方程若 ,則方程(2)中不出現奇異積分,因而方程(2)就是 具有弱奇異性核的弗雷德霍姆型積分方程;當 時,則稱方程(2)為 完整的奇異積分方程。如果 ,則稱(2)為 齊次的奇異積分方程;否則稱之為 非齊次的奇異積分方程。
特徵方程與相聯方程
積分方程
 柯西奇異積分方程
柯西奇異積分方程稱為奇異積分方程(2)的 特徵方程。
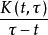 柯西奇異積分方程
柯西奇異積分方程 柯西奇異積分方程
柯西奇異積分方程 柯西奇異積分方程
柯西奇異積分方程把奇異積分方程(1)中的核 的變數 和 的位置互換,所得到的新的奇異積分方程
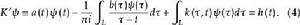 柯西奇異積分方程
柯西奇異積分方程稱為積分方程(2)的 轉置(或相聯)方程,而特徵方程(3)的相聯方程為
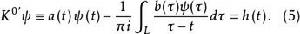 柯西奇異積分方程
柯西奇異積分方程 柯西奇異積分方程
柯西奇異積分方程註:當積分方程(3)中的係數 滿足條件
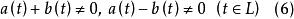 柯西奇異積分方程
柯西奇異積分方程時,則稱數
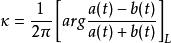 柯西奇異積分方程
柯西奇異積分方程為 特徵方程(3)的 指標。
性質
柯西奇異積分方程與弗雷德霍姆積分方程之間有著本質的不同。
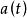 柯西奇異積分方程
柯西奇異積分方程對 弗雷德霍姆積分方程而言,如果齊次方程有異於零的解,則非齊次方程一般來說無解;而當齊次方程無異於零的解時,則非齊次方程對任意自由項總解。但對 柯西奇異積分方程而言情況就不一樣,如果齊次方程有異於零的解,則非齊次方程對任意的自由項也是可解的;而當齊次方程只有零解時,非齊次方程一般來說是無解的。 此外,柯西奇異積分方程的係數 可以為零,只要滿足條件(6)就可以求其解;但對弗雷德霍姆方程來說,如果積分號外不出現未知函式(即為第一種積分方程),一般地,它是不適定的。
重要定理
關於柯西奇異積分方程,諾特(Noether,F.)建立了下面的三個基本定理,這些定理起著與弗雷德霍姆積分方程的弗雷德霍姆理論相同的作用:
1.齊次奇異方程
 柯西奇異積分方程
柯西奇異積分方程的線件獨立(非零)解的個數是有限的。
2.奇異積分方程(2)可解的充分必要條件是滿足
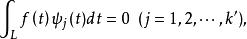 柯西奇異積分方程
柯西奇異積分方程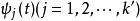 柯西奇異積分方程
柯西奇異積分方程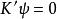 柯西奇異積分方程
柯西奇異積分方程其中 是相聯齊次方程 的線性無關解的完全組。
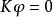 柯西奇異積分方程
柯西奇異積分方程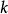 柯西奇異積分方程
柯西奇異積分方程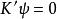 柯西奇異積分方程
柯西奇異積分方程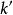 柯西奇異積分方程
柯西奇異積分方程 柯西奇異積分方程
柯西奇異積分方程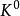 柯西奇異積分方程
柯西奇異積分方程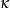 柯西奇異積分方程
柯西奇異積分方程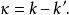 柯西奇異積分方程
柯西奇異積分方程3.齊次奇異方程 的線性無關解的個數 與其相聯齊次奇異方程 的線性無關解的個數 之差,僅依賴於運算元 的特徵部分,且等於 的指標 ,即
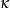 柯西奇異積分方程
柯西奇異積分方程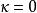 柯西奇異積分方程
柯西奇異積分方程弗雷德霍姆積分方程的弗雷德霍姆理論與柯西奇異積分方程的諾特理論的主要差別在於:在弗雷德霍姆積分方程中,齊次方程與其相聯齊次方程線性獨立解的個數相同;而對柯西奇異積分方程,兩者的個數一般不相等,其差等於奇異積分方程的指標 .特別地,如果 ,則諾特諸定理就是弗雷德霍姆理論的諸定理。
