概要介紹
問題背景
受隨時間變化的外載 p( t)和粘性阻尼作用下的線性單自由度(SDF )系統的運動方程是一個二階常微分方程,可寫為
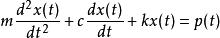 杜哈梅積分
杜哈梅積分其中m為等效振子的質量,x代表系統振幅,t代表時間,c是粘性阻尼係數,k是系統剛度。
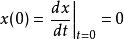 杜哈梅積分
杜哈梅積分若初始靜止於平衡位置的系統在t=0時刻受到一個單位衝擊載荷作用,即p(t)是一個狄拉克δ函式δ(t),,可以解得系統回響(稱為單位脈衝回響函式)為
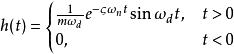 杜哈梅積分
杜哈梅積分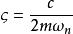 杜哈梅積分
杜哈梅積分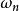 杜哈梅積分
杜哈梅積分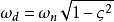 杜哈梅積分
杜哈梅積分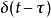 杜哈梅積分
杜哈梅積分其中稱為系統的阻尼比,是系統在無阻尼狀態下振動的固有圓頻率,是系統在當前存在的阻尼c作用下的實際振動圓頻率。推廣到任意時刻τ時受到衝擊載荷作用的脈衝回響為
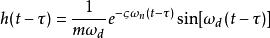 杜哈梅積分
杜哈梅積分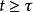 杜哈梅積分
杜哈梅積分,
結論導出
將任意載荷p(t)視為一系列脈衝激勵的迭加 :
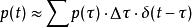 杜哈梅積分
杜哈梅積分那么根據線性性質可知,系統的回響同樣可以表示成對這一系列脈衝激勵的回響函式的迭加:
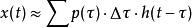 杜哈梅積分
杜哈梅積分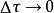 杜哈梅積分
杜哈梅積分在時,連續求和轉化為積分,此時上面的等式是嚴格成立的
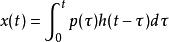 杜哈梅積分
杜哈梅積分將h(t-τ)的表達式代入即得杜哈梅積分的一般形式:
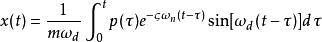 杜哈梅積分
杜哈梅積分