定義
對於給定的 n個 n-1次連續可微函式， f、...、 f，它們的朗斯基行列式 W(f, ..., f)為：
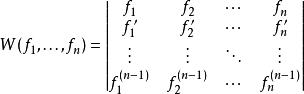朗斯基行列式行列式的第 i行是 f、...、 f各函式的 i-1次導數。組成這個行列式的 n階方陣也稱作這 n個函式的 基本矩陣。
在解線性微分方程時，朗斯基行列式可以用阿貝爾恆等式來計算。
與線性無關解
朗斯基行列式可以用來確定一組函式在給定區間上的線性相關性。
對於 n個 n-1次連續可微函式 f、...、 f，它們的朗斯基行列式 W(f, ..., f):
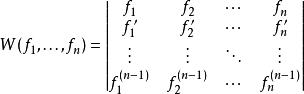朗斯基行列式定理：
如果f1、...、fn 在一個區間[a,b] 上線性相關，則W(f1, ..., fn) 在區間[a, b] 上恆等於零。
也就是說，如果在某些點上 W(f, ..., f) 不等於零，則 f、...、 f 線性無關
注意，若 W(f, ..., f)在區間 [ a, b] 上恆等於零，函式組 不一定線性相關。
線性微分方程
描述
考慮 n階線性微分方程：
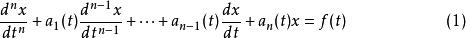朗斯基行列式
朗斯基行列式其中是區間 [ a, b] 上的連續函式。並考慮f(t)=0，即 n階齊次線性微分方程的情形：
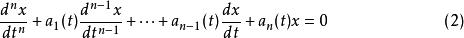朗斯基行列式對於一組給定的初始值：
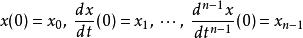朗斯基行列式
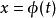朗斯基行列式 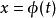朗斯基行列式方程 (1) 有唯一解。如果初始值不定的話，(2) 的任一解加上仍然是 (1) 的解。而對於 (2) ，任意 k個 (2) 的解的和仍然是 (2) 的解，因此 (2) 的解集構成一個線性空間，稱為 (2) 的 解空間。
定理的證明
朗斯基行列式如果 f、...、 f在一個區間 [ a, b] 上線性相關，則存在不全為零的係數使得對區間 [ a, b] 上的任意 t，
朗斯基行列式因為“微分”是線性運算元，所以這個等式可以“延伸”到n-1階導數。故有以下方程組：
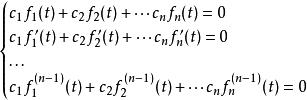朗斯基行列式 朗斯基行列式將看作變數，則上式變為一個 n元齊次線性方程組，由於這個方程有非零解，係數矩陣的行列式 W(f, ..., f)= 0。
進一步可以證明， W(f, ..., f)要么在區間 [ a, b] 上恆等於零，要么處處不為零（沒有零根）。於是可以證明 (2) 有 n個線性無關的解，並且它們線性張成的空間就是 (2) 的解空間。所以， (2) 的解空間是一個 n維線性空間。 (2) 一組 n個線性無關的解稱作它的一個 基本解組。
例子
1.考慮三個函式：1、 x和 x，在任意一個區間上，他們的朗斯基行列式是：
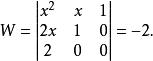朗斯基行列式不等於零，因此，這三個函式在任一個區間上都是線性無關的。
2.考慮另三個函式：1、 x和2 x+3，在任意一個區間上，他們的朗斯基行列式是：
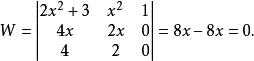朗斯基行列式事實上三者線性相關。
3.上面已經提到，朗斯基行列式等於零的函式組不一定線性相關。下面是一個反例：考慮兩個函式， x和| x|，即 x的絕對值。計算兩者的朗斯基行列式
朗斯基行列式他們的朗斯基行列式恆等於零，但兩者顯然線性無關。
