基本解組

基本解組是指能用線性組合構造出齊次線性微分方程全部解的線性無關的解系。微分方程基本解組的存在性是由微分方程的基本理論保證的，而方程的 n 個解的線性無關性則可以通過朗斯基行列式準則加以判定。

簡介

n 階齊次線性微分方程組

考慮 n 階齊次線性微分方程組

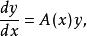基本解組

其中矩陣

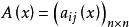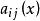基本解組

基本解組

中的每個元素 都是區間 a<x<b 上的連續函式，

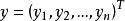基本解組

該方程在區間 a<x<b 上有 n 個線性無關的解

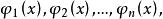基本解組

其通解為

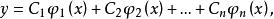基本解組

其中 C,C,...,C為任意常數。

方程組的任意一組 n 個線性無關的解稱為它的一個基本解組。

線性齊次微分方程

對於線性齊次微分方程，也有類似的概念：考慮 n 階線性齊次微分方程

基本解組

其中係數函式 a(x)(k=1,...,n) 在區間 a < x < b 上連續。該方程在區間a < x < b 上有 n 個線性無關的解，而且其通解可以由這 n 個解的線性組合表示。稱方程的任意 n 個線性無關的解為該方程的一個基本解組。

判定

微分方程基本解組的存在性是由微分方程的基本理論保證的，而方程的 n 個解的線性無關性則可以通過朗斯基行列式準則加以判定。