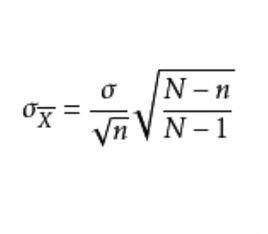基本介紹
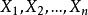 有限總體修正係數
有限總體修正係數 有限總體修正係數
有限總體修正係數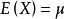 有限總體修正係數
有限總體修正係數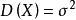 有限總體修正係數
有限總體修正係數 有限總體修正係數
有限總體修正係數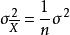 有限總體修正係數
有限總體修正係數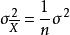 有限總體修正係數
有限總體修正係數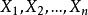 有限總體修正係數
有限總體修正係數 有限總體修正係數
有限總體修正係數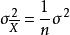 有限總體修正係數
有限總體修正係數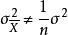 有限總體修正係數
有限總體修正係數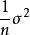 有限總體修正係數
有限總體修正係數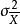 有限總體修正係數
有限總體修正係數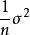 有限總體修正係數
有限總體修正係數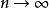 有限總體修正係數
有限總體修正係數設是無限總體X的隨機樣本,樣本平均數為,若已知總體X的數學期望,方差,容易推出的抽樣分布的方差是,這個公式只適用於無限總體,或者總體雖是有限但抽樣是有放回的情形。此時,樣本的n個個體被看作n個獨立同分布的隨機變數,因此有式的成立。但是,在實際中,經常遇到的是對有限總體採用無放回抽樣,此時抽樣所構成的樣本就不能假定為相互獨立的隨機變數。因此,樣本方差的公式就不再適用,此時,而是應小於。這是因為當總體容量為N時,在樣本容量n→N時趨向於0,而只有在時,才趨向於0 。
 有限總體修正係數
有限總體修正係數因此,當總體為有限時,的方差要乘上一個修正係數
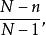 有限總體修正係數
有限總體修正係數即
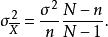 有限總體修正係數
有限總體修正係數 有限總體修正係數
有限總體修正係數同理的標準差
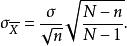 有限總體修正係數
有限總體修正係數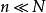 有限總體修正係數
有限總體修正係數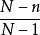 有限總體修正係數
有限總體修正係數由於當時,修正係數接近於1。故一般情況當n≤0.05N時,即樣本容量不大於總體容量的5%時,可以不用有限總體的修正係數 。
使用條件及說明
由於n永遠是大於1的,所以有限總體修正係數永遠小於1,因此,有限總體的抽樣平均誤差比無限總體的抽樣平均誤差要小。對無限總體來說,樣本在總體中所占的比重相對來說是極微小的,所以在無限總體中抽取的樣本代表性要差一些,其抽樣誤差大於有限總體的抽樣誤差,也正好說明了這個問題。
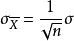 有限總體修正係數
有限總體修正係數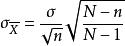 有限總體修正係數
有限總體修正係數當有限總體的N相對於樣本容量n很大時,有限總體修正係數將接近於1,這時有限總體的抽樣平均誤差接近於無限總體的抽樣平均誤差。為了簡化計算過程,在這種情況下,可以直接採用公式,而省略公式。另外,n/N的比值稱為抽樣比例。在統計學上,通常認為抽樣比例n/N<0.05時,就可以省略有限總體修正係數。當n/N≥0.05時,則認為總體相對於樣本來說,並不很大,或稱為有限總體。這時一般要使用有限總體修正係數。
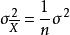 有限總體修正係數
有限總體修正係數 有限總體修正係數
有限總體修正係數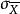 有限總體修正係數
有限總體修正係數另外,公式除了具有計算簡便的優點以外,它還有一個優點,就是式中的總體標準差是個常量,抽樣平均誤差的大小僅僅取決於抽樣單位數目,與總體容量N無關 。