詳述
系統中微觀粒子一般具有一系列離散的能量,記這些能量為
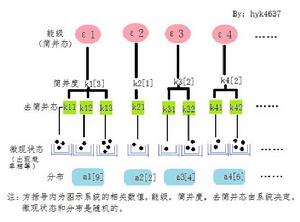
這些處於相同能量的粒子還可能具有不同的其他微觀物理量,比如同具有動能ε的一維自由粒子動量具有兩個相反的方向。這時,能量是簡併的,而動量是非簡併的。記每個能量下細化到非簡併時的狀態數目分別為k1,k2,……,kn,……={kn} ,稱每一個k是該能量的簡併度。上述例子相應的能量簡併度為2。
某一個分布下的微觀狀態數,即該分布下系統所有可能出現的微觀狀態的總數(微觀狀態概念參見等機率原理或被詞條附圖),用符號Ω標記。對於每一個分布(見上文),它只規定了每種能量下的粒子數,而許多微觀狀態都滿足這種分布。這些微觀狀態也是隨時間不停發生變化。一種分布下的全部可能的微觀狀態數目是可以被計算出來的。這種一對多的關係來源於能量的簡併(見上文),可分辨和不可分辨全同粒子的特性和泡利不相容原理等等。
根據等機率原理,各個分布下的所有的微觀狀態出現的機率都一樣,因此,分布包含的可能微觀狀態數目Ω越多時,該分布出現的機率就越大。最大的Ω對應機率最大的分布,該分布稱為最概然分布
對於一個系統,微觀粒子每時每刻都在變化,各種分布都會出現,但它們出現的機率不同(如上文所述,原因被抽象為該分布下微觀狀態數不同),物理學用出現機率最大的一個分布(最概然分布)來代替當前系統微觀粒子的分布,而忽略其他分布出現的可能。這種處理是合理的,因為計算表明,當粒子數足夠大時,最概然分布出現的機率遠遠高於其他分布出現的機率。
分布與微觀狀態數Ω有關,而Ω又與{an}和{kn}有關,具體關係參見。而最概然{an}又和系統總能量,系統粒子總數,{kn}和{εn}有關,所以巨觀和微觀在數學上就被聯繫起來,進而可以討論它們在物理上的聯繫。
著名的麥柯斯韋-波爾茲曼分布,是在最概然分布的物理意義下產生的,它只是眾多分布中的一個極大值。這之後出現的費米-狄拉克分布和玻色-愛因斯坦分布也是一個最概然分布,無論是用經典方法還是系綜理論,都離不開最後這步處理。這三個分布的區別在於各自的微觀狀態數的表達式不同,因為描述這三種分布下粒子的限定條件不同。具體請參見
