最大值原理的內涵
設系統的狀態方程為:
 最大值原理
最大值原理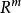 最大值原理
最大值原理控制u屬於 中的某個有界閉集U,最優控制問題是求u∈U,使得
 最大值原理
最大值原理最小。
 最大值原理
最大值原理假設f(x,u,t)的分量為 並假設
 最大值原理
最大值原理都是其自變數的連續函式。用u*、x*分別表示最優控制和最優軌跡,則u*使J(u)取最小值的必要條件是:
(1)存在協狀態向量λ*(t),它和x*(t),u *(t)一起滿足正則方程
 最大值原理
最大值原理(2)哈密頓函式作為u的函式在u=u*(t)取最小值,即
 最大值原理
最大值原理(3)正則方程的邊界條件:
 最大值原理
最大值原理a.若 是給定的,則邊界條件為
 最大值原理
最大值原理b.如果tf給定,x(tf)自由,那么邊界條件為
 最大值原理
最大值原理c.如果tf也是自由的,還要加一個條件:
 最大值原理
最大值原理以確定tf。
d.如果要求x(tf)落在m維流型S上,
 最大值原理
最大值原理那么邊界條件為
 最大值原理
最大值原理如果tf是自由的,再增加條件
 最大值原理
最大值原理可以看出,上述的正則方程和邊界條件與u無約束的情況用變分法導出的完全相同。
最大值原理與哈密頓函式
如果最優控制問題是求u∈U,使得目標函式J(u)最大,在最大值原理中,最優控制u*應使哈密頓函式值最大,即
 最大值原理
最大值原理對區間[t0 ,tf]上的所有t成立,其含義是:對於由最優控制u=u*(t)引發的x*(t)和協狀態λ*(t),哈密頓函式作為u函式,在u=u*(t)處取最小值。
在u為標量的情況,必要條件的含義是:在特定的時刻t和特定的x*(t)、λ*(t)曲線,哈密頓函式的右端可以看做u的函式,最優控制u*(t)使它取最小值
 最大值原理
最大值原理當U為閉區間[a,b]時,允許的控制滿足
 最大值原理
最大值原理哈密頓函式僅作為u的函式,有如圖所示的三種情況:
 最大值原理
最大值原理第一種情況:哈密頓函式的最小值在區間[a,b]內的點達到。如果哈密頓函式關於u是可微的,則必要條件為
 最大值原理
最大值原理其他兩種情況是哈密頓函式的最小值在區間[a,b]的邊界點達到,這時則必須用更廣泛的條件
 最大值原理
最大值原理也就是用條件
 最大值原理
最大值原理來描述。
最大值原理求最優策略的步驟
當x(tf)是自由的時,套用最大值原理求最優策略的具體步驟如下:
第1步:構造系統的哈密頓函式為
 最大值原理
最大值原理第2步:由
 最大值原理
最大值原理導出決策變數u與狀態變數x、協狀態變數λ的關係,記為u=u(x,λ)。
第3步:寫出以下正則(正規)方程組為
 最大值原理
最大值原理將u=u(x,λ)帶入正則方程,解出x=x*(t),λ=λ*(t)。
第4步:將x=x*(t),λ=λ*(t)代入u=u(x,λ)得到最優策略
 最大值原理
最大值原理如果決策問題還要求滿足邊界條件x(tf)=xf ,則以這個邊界條件取代正則方程組中的條件:
 最大值原理
最大值原理最大值原理的局限性
最大值原理雖然解決了古典變分法所遇到的困難,但是它也只給出了最優控制問題解的必要條件,而不是充分條件,所以由最大值原理所求的控制函式不一定是最優控制,因為有可能最優控制根本不存在。如果最優控制問題的解存在,但是從這方法得到的控制函式不止一個,就需要進行逐個檢驗,從中確定出最優解,如果該問題的實際物理背景有最優控制,而從最大值原理得到的解又只有一個,那么這個解一定是最優控制 。
