詳解
簡單來說，此定理是指在所有可能的控制中，需讓“控制哈密頓量”（control Hamiltonian）取極值，極值是最大值或是最小值則依問題以及哈密頓量的符號定義而不同。 正式的用法，也就是哈密頓量中所使用的符號，會取到最大值，但是此條目中使用的符號定義方式，會讓極值取到最小值。
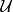龐特里亞金最大化原理
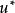龐特里亞金最大化原理若是所有可能控制值的集合，則此原理指出，最優控制必須滿足以下條件：
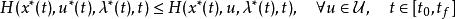龐特里亞金最大化原理
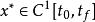龐特里亞金最大化原理
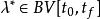龐特里亞金最大化原理其中是最佳狀態軌跡，而是最佳協態軌跡
此結果最早成功的套用在輸入控制有限制條件的最小時間問題中，不過也可以用在狀態有限制條件的問題中。
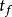龐特里亞金最大化原理
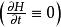龐特里亞金最大化原理也可以推導控制哈密頓量的特殊條件。若最終時間固定，且控制哈密頓量不是時間的顯函式，則：
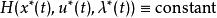龐特里亞金最大化原理若最終時間沒有限制，則：
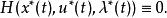龐特里亞金最大化原理若在某一軌跡上滿足龐特里亞金最大化原理，此原理是最佳解的必要條件。哈密頓-雅可比-貝爾曼方程提供了最佳解的充份必要條件，但該條件須在整個狀態空間中都要成立。
最大化和最小化
此定理一開始的名稱是 龐特里亞金最大化原理（Pontryagin's maximum principle），其證明也是以控制哈密頓量最大化為基礎。此原理最早的套用是要最大化火箭的終端速度。不過後來此定理大部分的套用是使性能指標最小化，因此常稱為龐特里亞金最小化原理。龐特里亞金的書解出了要讓性能指標最小化的問題
最小化問題必要條件的正式敘述
龐特里亞金最大化原理
龐特里亞金最大化原理以下是讓泛函最小化的必要條件。令為在輸入為時，動態系統的狀態，且滿足以下條件
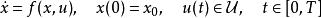龐特里亞金最大化原理其中
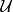龐特里亞金最大化原理為可行控制的集合
龐特里亞金最大化原理為系統的結束時間。
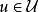龐特里亞金最大化原理
龐特里亞金最大化原理
龐特里亞金最大化原理 龐特里亞金最大化原理控制需在所有內使目標泛函最小化，目標泛函隨套用而定，可以寫成
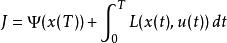龐特里亞金最大化原理
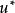龐特里亞金最大化原理 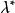龐特里亞金最大化原理
龐特里亞金最大化原理
龐特里亞金最大化原理龐特里亞金最小化原理提到最佳狀態軌跡，最佳控制及對應的拉格朗日乘數向量必需最小化哈密頓量，因此
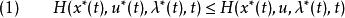龐特里亞金最大化原理 龐特里亞金最大化原理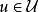 龐特里亞金最大化原理針對所有時間，也針對所有可能的控制輸入。以下的式子也必須成立
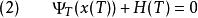龐特里亞金最大化原理而且也要滿足以下的協態方程
龐特里亞金最大化原理若最終狀態{\displaystyle x(T)}沒有固定（其微分變異不為0），最終協態也要滿足以下條件
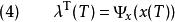龐特里亞金最大化原理
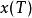龐特里亞金最大化原理 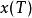龐特里亞金最大化原理上述(1)-(4)的條件是最佳控制的必要條件。公式(4)只有在沒有固定時才需要成立。若是固定值，公式(4)不在必要條件中。
此解法可以套用在宇宙學和天體物理學中。
