復簡諧
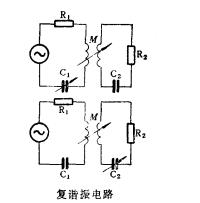 圖1
圖1![最佳耦合[電工學領域]](/img/f/db3/nBnauM3XzETO5IjNxgDM0YTN1UTM1QDN5MjM5ADMwAjMwUzL4AzLzUzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 最佳耦合[電工學領域]
最佳耦合[電工學領域]在如圖1所示互感耦合電路中,調節任一個迴路的電抗(如調C1或C2)、電路之間的耦合(調M),使次級迴路電流達到可能達到的最大值,其最大值 ,這種讓一個迴路諧振並選擇最佳耦合的調諧叫做復諧振。
全諧振
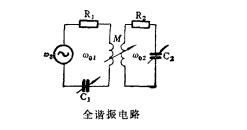 圖2
圖2![最佳耦合[電工學領域]](/img/f/db3/nBnauM3XzETO5IjNxgDM0YTN1UTM1QDN5MjM5ADMwAjMwUzL4AzLzUzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 最佳耦合[電工學領域]
最佳耦合[電工學領域]調節初次級迴路的電抗(調C1和C2),及初次級間的耦合(調M),使次級迴路電流達到可能達到的最大值,其最大值 。這種將兩迴路都調諧到信號頻率,而且選擇了最佳耦合的調諧叫做全諧振。
耦合電路
兩個或兩個以上的迴路構成一個網路時,其中某一電路中電流或電壓發生變化,能影響到其它電路也發生類似變化。這種網路叫做耦合電路。實現耦合的條件是,電路彼此之間具有公共阻抗,通過這個公共阻抗將能量從一個迴路傳輸到另一個迴路。根據公共阻抗的性質不同分為:電阻耦合,電容耦合,電感耦合,互感耦合等多種耦合方式。如果初、次級都是由電感電容並聯組成的振盪迴路稱為雙調諧耦合電路;如果初、次級
只有一個迴路是由電感電容組成的振盪迴路,稱為單調諧耦合電路。
諧振
在由電感和電容所組成的電路中,在外加激勵源的作用下將激起振盪。調節電感或電容值,或改變激勵源的頻率可使得激勵電壓和電路電流同相。這個情況稱為諧振。在諧振時,電路呈現一純電阻,且振盪最強。、
最佳耦合電路是在復諧振、全諧振時候的電路。
最佳耦合曲線
電感耦合迴路,耦合鬆了成雙峰諧振曲線,耦合緊了成單峰窄頻帶諧振曲線,耦合適中才成最佳耦合諧振曲線,放大量和頻帶都比較合適,輸出功率最大,中頻放大器迴路往往採用三級參差調諧效果最好。在無線電系統中,由整體到單機,由單機到元件,幾乎隨處都可以看到三極對立統一的客觀存在。
雷射器的閾值和最佳耦合輸出
當外加激勵的能源功率(光能源或電能源)超過某一臨界值時,雷射物質中的粒子數反轉達到了一定程度,雷射器才能克服光諧振腔內的損耗而產生雷射,此臨界值就稱為雷射器的閾值。閾值可以有能量閾值、功率閾值,電流閾值等名稱。
當外加激勵能源達到閾值時,單位體積內雷射物質的高能級原子數與低能級原子數之差,稱作閾值反轉密度。
一般多能級系統的閾值密度要低些。例如:二能級系統的雷射物質,很難達到粒子數反轉;三能級系統的(如紅寶石雷射器)達到閾值時,所需要的高能級的原子數比四能級系統(如釹玻璃雷射器,摻釹釔鋁石榴石雷射器等)達到閾值時所需要的高能級原子數高得多。圖2表示了幾種固體雷射器的閾值反轉密度的典型數據。
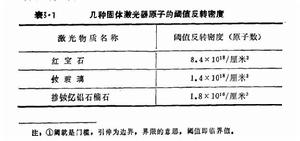 圖2
圖2在實際使用中,外加激勵源剛達到閾值時,雖有雷射輸出,但很弱,一般總是在高於閾值水平上工作。我們希望閾值越小越好,因為閾值小,所要求的外加激勵的能源就小,雷射器件本身發熱就少,把其它能量轉為光能的效率就高,容易產生連續振盪。在長距離通信中,中繼器中所用雷射器的遠供電源也容易解決,這是具有重要意義的。
![最佳耦合[電工學領域]](/img/0/43e/nBnauM3XzUzN0ETN2IzNzYTN1UTM1QDN5MjM5ADMwAjMwUzLyczLzUzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 最佳耦合[電工學領域]
最佳耦合[電工學領域]製作雷射器要求有較大的雷射功率輸出。以兩平行平面鏡組成的諧振腔為例來說,就需要減小部分透射鏡M2的反射率R2,以求射出M2反射鏡的雷射強些。但因 ,這樣Q值就要減小,相當於腔內光損耗增大。當光損耗超過光的增益時,腔內雷射振盪就會衰減到零,而停止振盪。所以在雷射器的諧振腔中存在著最佳耦合輸出的問題。也就是在兩反射鏡所組成的雷射器中,部分反射鏡M2的反射率R2有一個最佳值的選擇問題,這可以在製作雷射器時,通過實驗來確定。
光泵閾值和最佳耦合
重複頻率的脈衝器件一般是高增益、低反饋的器件,光泵閾值和最佳耦合要求不太嚴格。而連續固體器件一般是低增益、高反饋的器件,因而光泵閾值和最佳耦合的要求比一般脈衝器件的要求較嚴格。這也是連續固體器件和重複頻率脈衝器件的一個差別。因此在雷射器的設計上這一點應該分別考慮。對於重複頻率脈衝器件,前面討論過的脈衝器件設計原理,原則上都可適用,我們不再敘述了。這一節我們想著重於固體連續器件的特點,結合實例討論其光泵閾值和最佳耦合問題,並導出用實驗來判斷雷射材料優劣的方法和判據。
一般固體雷射器的效率都是低的,高重複頻率和連續器件也不例外。以優質釔鋁石榴石晶體為例,它所能達到的總體效率也不過百分之二、三。氪弧燈的電光轉換效能約40%,經聚光器反射又損失一部分,而在整個發光譜中只有一小部分被釔鋁石榴石吸收,轉化為我們所需要的螢光。從氪燈輸入的電能轉換為摻釹釔鋁石榴石的1.064微米螢光的效能僅為5~6%。
沒有雷射共振腔時,被光泵抽運到起始能級3的粒子只有通過自發輻射回到能級2,所發出的螢光是雜亂無章的。如果有雷射共振腔,在開始的瞬間,工作物發出的還是各個方向的螢光,不過其中沿雷射腔軸進行的那一部分光子不易消失,被反射鏡反射回來通過工作物質時,使部分起始能級粒子產生受激輻射,山受激輻射所產生光子的方向、頻率和相位與原來的光子一樣。增添的光子使原來這一類型的電磁場增強一些,受激輻射躍遷幾率也相應增大一些,也就迫使更多高能級粒子產生受激輻射。這樣就象滾雪球似的,使雷射越來越強。雷射增益是由高能態粒子反轉數決定的,可以用下式表示:
![最佳耦合[電工學領域]](/img/d/2fa/nBnauM3X0ETMzgzMzEDM0YTN1UTM1QDN5MjM5ADMwAjMwUzLxAzL1YzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 最佳耦合[電工學領域]
最佳耦合[電工學領域]其中:
![最佳耦合[電工學領域]](/img/8/f77/nBnauM3X1EDO4kTNwMTMzEDN0UTMyITNykTO0EDMwAjMwUzLzEzLwMzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 最佳耦合[電工學領域]
最佳耦合[電工學領域]——吸收截面;
![最佳耦合[電工學領域]](/img/0/c9a/nBnauM3XyEDOygTNzAzMyADN0UTMyITNykTO0EDMwAjMwUzLwMzLzIzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 最佳耦合[電工學領域]
最佳耦合[電工學領域]——棒長;
![最佳耦合[電工學領域]](/img/4/32b/nBnauM3XzcDO0MDNxMDOxUTN1UTM1QDN5MjM5ADMwAjMwUzLzgzL1czLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 最佳耦合[電工學領域]
最佳耦合[電工學領域]——粒子反轉數。
![最佳耦合[電工學領域] 最佳耦合[電工學領域]](/img/7/8ee/nBnauM3X1ATM3gjNycjMxADM2UTM1QDN5MjM5ADMwAjMwUzL3IzLwczLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg)
