曲邊梯形

曲邊梯形有三條邊是直線，其中兩條互相平行，第三條與前兩條互相垂直，第四條邊是一條曲線的一段弧，它與任一條平行於它的鄰邊的直線至多只交於一點。可利用定積分求曲邊梯形面積。

定義

五十年代蘇聯A·jI辛飲著的《數學分析簡明教程》，其中對曲邊梯形是這樣定義的：它有三條邊是直線，其中兩條互相平行，第三條與前兩條互相垂直，第四條邊是一條曲線的一段弧，它與任一條平行於它的鄰邊的直線至多只交於一點。

高等數學：由直線 x=a，x=b(a≠b)，y=0和曲線y=f(x)所圍成的，稱之為曲邊梯形。

計算

面積

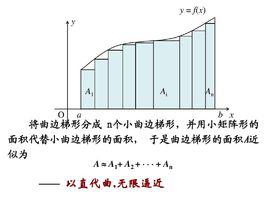
1.用極限逼近原理求曲邊梯形的面積，是一種“以直代曲”的思想，它體現了對立統一，量變與質變的辨證關係.

2.求曲邊梯形的面積的基本思路是：把曲邊梯形分割成n個小曲邊梯形→用小矩形近似替代小曲邊梯形→求各小矩形的面積之和→求各小矩形面積之和的極限.

圖形

可利用定積分求曲邊梯形面積

公式：∫ f(x)dx

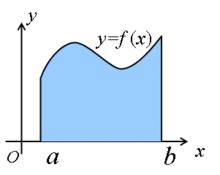曲邊圖形