定律定義
二維的情形
(1)平面上的單連通區域與復連通區域
 曲線積分與路徑無關性
曲線積分與路徑無關性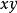 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性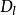 曲線積分與路徑無關性
曲線積分與路徑無關性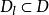 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性設 是平面 上的區域。如果 內的任何封閉曲線 所圍成的區域 ,恆有 ,則 稱為單連通區域;否則, 稱為復連通區域。
(2)平面曲線積分與路徑無關的條件
 曲線積分與路徑無關性
曲線積分與路徑無關性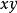 曲線積分與路徑無關性
曲線積分與路徑無關性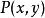 曲線積分與路徑無關性
曲線積分與路徑無關性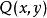 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性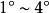 曲線積分與路徑無關性
曲線積分與路徑無關性定理1 設 是平面 上的單連通閉區域,函式 與 在 內具有一階連續偏導數,則下列 兩兩等價
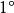 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性沿 內任何光滑閉曲線 ,恆有
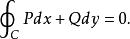 曲線積分與路徑無關性
曲線積分與路徑無關性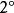 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性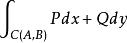 曲線積分與路徑無關性
曲線積分與路徑無關性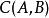 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性對 內的曲線積分 ,只與這光滑曲線 的起點 、終點 有關,而與路徑無關,即恆有
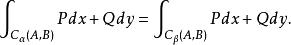 曲線積分與路徑無關性
曲線積分與路徑無關性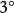 曲線積分與路徑無關性
曲線積分與路徑無關性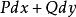 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性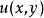 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性在 內是某一個函式 的全微分,即在 恆有
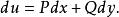 曲線積分與路徑無關性
曲線積分與路徑無關性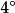 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性在 內每一點處恆有
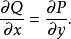 曲線積分與路徑無關性
曲線積分與路徑無關性三維的情形
(1)曲面單連通區域與曲面復連通區域
 曲線積分與路徑無關性
曲線積分與路徑無關性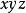 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性設 是 空間的區域。如果 內的任何簡單封閉曲線 ,都存在以 為邊界的曲面 ,使得 ,則 稱為曲面單連通區域;否則, 稱為曲面曲面復連通區域。
(2)空間曲線積分與路徑無關的條件
 曲線積分與路徑無關性
曲線積分與路徑無關性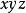 曲線積分與路徑無關性
曲線積分與路徑無關性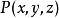 曲線積分與路徑無關性
曲線積分與路徑無關性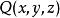 曲線積分與路徑無關性
曲線積分與路徑無關性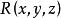 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性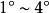 曲線積分與路徑無關性
曲線積分與路徑無關性定理2 設 是平面 空間的曲面單連通閉區域,函式 、 、 在 內都具有一階連續偏導數,則下列 兩兩等價
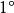 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性沿 內任何光滑閉曲線 ,恆有
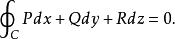 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性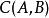 曲線積分與路徑無關性
曲線積分與路徑無關性對 內任何一個光滑曲線段 ,曲線積分
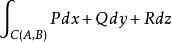 曲線積分與路徑無關性
曲線積分與路徑無關性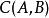 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性僅與 的起點 、終點 有關,而與路徑無關。
 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性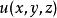 曲線積分與路徑無關性
曲線積分與路徑無關性在 內是某一個函式 的全微分,即在內恆有
 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性在 內每一點處恆有
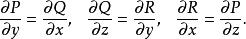 曲線積分與路徑無關性
曲線積分與路徑無關性套用領域
 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性上述兩類定理條件中要求 和 為單連通區域是很重要的。如下面的例子:
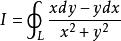 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性例 1 計算 ,其中 為任一不包含原點的閉區域 的邊界曲線,分段光滑.
解 因為
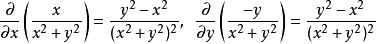 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性在區域 上連續且相等,於是
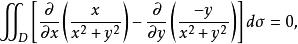 曲線積分與路徑無關性
曲線積分與路徑無關性所以根據格林公式即可得
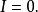 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性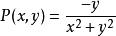 曲線積分與路徑無關性
曲線積分與路徑無關性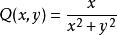 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性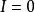 曲線積分與路徑無關性
曲線積分與路徑無關性 曲線積分與路徑無關性
曲線積分與路徑無關性倘若 為繞原點一周的封閉曲線,則函式 , 只在剔除原點外的任何區域 上有定義,所以 必含在某個復連通區域內。這時它不滿足定理1的條件,因而就不能保證 成立。事實上,設 為繞原點一周的圓
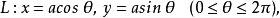 曲線積分與路徑無關性
曲線積分與路徑無關性則有
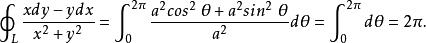 曲線積分與路徑無關性
曲線積分與路徑無關性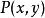 曲線積分與路徑無關性
曲線積分與路徑無關性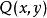 曲線積分與路徑無關性
曲線積分與路徑無關性若 , 滿足定理1的條件,則由上述證明可看到二元函式
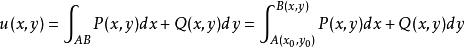 曲線積分與路徑無關性
曲線積分與路徑無關性具有性質
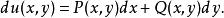 曲線積分與路徑無關性
曲線積分與路徑無關性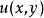 曲線積分與路徑無關性
曲線積分與路徑無關性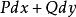 曲線積分與路徑無關性
曲線積分與路徑無關性它與一元函式的原函式相仿。所以我們也稱 為 的一個原函式。
