曲線坐標系
設（y ，y ，y ）為歐氏空間 R 中Descartes坐標系，Ω為 R 中的某一連通區域，Ω上給出三個連續可微、單值函式
x =f （y ，y ，y ），i=1，2，3，
如果可逆，有
y =g （x ，x ，x ），i=1，2，3。
此即，Ω上的變數（x ）和Descartes坐標系（y ）之間，由可逆、雙方單值、連續可微的變換聯繫著，則這樣的（x ）稱為Ω上的曲線坐標系。
在曲線坐標系中，指標有上下之分，帶上標的量為逆變數，帶下標的量為協變數，既有上標又有下標的為混合變數。
坐標變數{x ，x ，x }為逆變數，一般記為{x }。
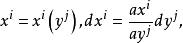曲線坐標可用矩陣表示如下：
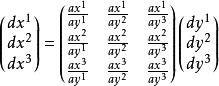曲線坐標形如 x=Ay，若︳ A︳≠0，則存在逆變換 y=Ax。同樣地，若
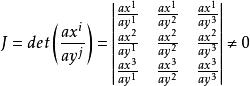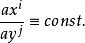曲線坐標
曲線坐標則x =x （y ）存在逆變換：y =y （x ），其中J稱為雅可比（Jacobi）行列式。實際上逆變換存在還需要一個條件：J≠0。當時，x =x （y ）是線性函式，（y ）是斜角坐標系。
空間曲線坐標系，由空間曲面組（坐標曲面）的交線確定。如圖1，三維情況：y =const.確定一曲面，稱為y 曲面；y =const.，y =const.分別為y ，y 曲面。在y 曲面和y 曲面的交線上，只有y 變化，這條交線稱為y 坐標曲線。同樣，可得y 坐標曲線和y 坐標曲線。
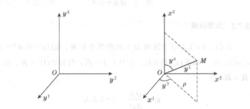圖1球面坐標系（y ，y ，y ）：
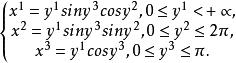曲線坐標如圖2，坐標面分別為
y =const.：球面，
y =const.：半平面，
y =const.：錐面。
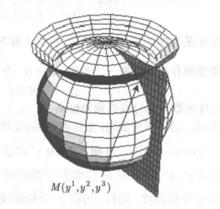圖2曲線坐標計算程式功能
1、本軟體可計算圓曲線帶有緩和曲線中、邊樁坐標及切線方位角，若只需計算圓曲線則緩和曲線輸入0即可。
2、附有正算、反算功能，正算：通過里程和偏距計算坐標，反算：通過坐標反推里程和偏距。
3、數據輸入：曲線轉角α和計算方位角F按 d.ms 格式輸入，如：-14°18ˊ10″則為：-14.1810，選擇“連續計算”時偏距和偏角同單點計算一致。
4、具有數據導入、導出功能，可把已知數據輸入在文本文檔中進行導入，導出則是把已經輸入好的數據導出到指定位置。
5、數據處理完畢後點擊“保存數據”可進行保存曲線五大樁、曲線參數表，連續計算模式“保存數據”可導出計算成果。
