簡介
 普朗克粒子
普朗克粒子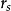 普朗克粒子
普朗克粒子普朗克粒子是一種假設的粒子,定義為約化康普頓波長等於半個史瓦西半徑的微黑洞。用方程表達,約化康普頓波長與史瓦西半徑分別為
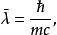 普朗克粒子
普朗克粒子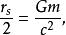 普朗克粒子
普朗克粒子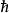 普朗克粒子
普朗克粒子 普朗克粒子
普朗克粒子 普朗克粒子
普朗克粒子 普朗克粒子
普朗克粒子其中,是約化普朗克常數,是普朗克粒子的質量,是光速,是萬有引力常數。
使兩個方程相等,可以得到普朗克粒子的質量:
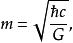 普朗克粒子
普朗克粒子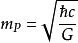 普朗克粒子
普朗克粒子所以,普朗克粒子的質量與普朗克質量的關係是
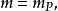 普朗克粒子
普朗克粒子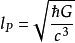 普朗克粒子
普朗克粒子而普朗克粒子的約化康普頓波長與普朗克長度的關係則是
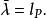 普朗克粒子
普朗克粒子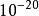 普朗克粒子
普朗克粒子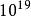 普朗克粒子
普朗克粒子與質子這類的粒子比較,普朗克粒子是極小極重的粒子;它的半徑大約是質子的半徑乘以,質量大約是質子的質量乘以。
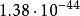 普朗克粒子
普朗克粒子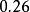 普朗克粒子
普朗克粒子許多物理學家認為普朗克粒子會因為霍金輻射而消失不見。依照理論估計,普朗克粒子的壽命只有秒,或普朗克時間。這么極短的一霎那時間,目前尚無法成功地測量。在另一方面,霍金輻射這理論仍舊存在著許多爭議,仍舊等待更多的研究與論證。
史瓦西半徑
史瓦西半徑(Schwarzschild radius)是任何具有質量的物質都存在的一個臨界半徑特徵值。在物理學和天文學中,尤其在萬有引力理論、廣義相對論中,它是一個非常重要的概念。1916年卡爾·史瓦西首次發現了史瓦西半徑的存在,這個半徑是一個球狀對稱、不自轉又不帶電荷的物體的重力場的精確解。該值的含義是,如果特定質量的物質被壓縮到該半徑值之內,將沒有任何已知類型的力(如簡併壓力)可以阻止該物質自身的重力將自己壓縮成一個奇點。
對符合條件(即不自轉、不帶電)的任何物體的史瓦西半徑皆與其質量成正比。理論上,太陽的史瓦西半徑約為3公里,地球的史瓦西半徑只有約9毫米。
一個不少於3.2個太陽質量的星體一旦坍縮至小於它的史瓦西半徑便會因為自身重力坍縮成為一點,從而變成黑洞。對於一個已經形成的黑洞來說,若將史瓦西半徑內的物質看作一個系統,則該系統內的任何物質都無法逃逸出該半徑之外。換句話說,該半徑也是不帶電荷無自轉黑洞的視界,光和粒子均無法逃離這個球面。由於黑洞的無毛性(即我們無法得到有關黑洞內部的有效信息),再加上目前所知的科學定律在史瓦西半徑內均會失效,因此我們無法觀測或者預測史瓦西半徑內的事件。也就是說,我們無法確切知道黑洞內是否存在一個由某種物質組成的球體,如果存在的話,其球體的半徑是多少。正因如此,視界通常被認為是黑洞的表面。又因為黑洞視界本身並不好直接測量,史瓦西半徑等類似方法就作為估算視界半徑的方法。銀河中心的超大質量黑洞的史瓦西半徑估計約為780萬公里。一個平均密度等於臨界密度的球體的史瓦西半徑等於我們的可觀測宇宙的半徑,也就是說如果可觀測宇宙的平均密度為臨界密度,其本身可被理解為一個黑洞。
然而,旋轉黑洞、帶電荷黑洞及旋轉並帶電黑洞的解則較為複雜,在不同的條件下,它們可以有兩層、一層或者甚至沒有視界。
微型黑洞
微型黑洞,又稱作 量子黑洞(quantum mechanical black holes)或者 迷你黑洞,是很小的黑洞。被稱作量子力學黑洞是因為在這個尺度之下,量子力學的效應扮演了非常重要的角色。
有可能這些量子層級的原生黑洞是在早期的宇宙(或者大爆炸時期)裡面高密度的環境,或者是在隨後的相變裡面被產生出來。透過因霍金輻射效應所預計散射出的粒子,在不遠的未來,說不定天文物理學家可以觀測到這些黑洞。
有些涉及到多次元的理論,預測存在一些微型黑洞的質量可以小到電子伏特的範圍,這種程度的能量可以在像是LHC(大型強子對撞機,Large Hadron Collider)這種粒子對撞機裡面產生出來。因此有一些大眾擔心這會導致世界末日(參見大型強子對撞機粒子對撞實驗的安全性)。然而,這種量子黑洞會很快的蒸發(evaporate)掉,僅僅留下很小的互動作用或者全部消失。而且除了這些理論之外,我們注意到射向地球的宇宙線並沒有對地球產生任何傷害,即使這些宇宙線的質心帶有的能量也高達了數百TeV。
參閱
•微黑洞
•普朗克單位
•自然單位
