簡介
在理論物理學裡, 明顯對稱性破缺(explicit symmetry breaking)是對稱性破缺的一種。假若系統的哈密頓量或拉格朗日量本身存在一個或多個違反某種對稱性的項目,導致系統的物理行為不具備這種對稱性,則稱此為 明顯對稱性破缺。這術語特別適用於大致具有對稱性、違反對稱項目很小的系統。
這類的項目有許多種可能的來源:
在理論或實驗的基礎上,直接加入破壞對稱項目。最著名的例子,如量子場論中的弱互動作用破壞了宇稱的對稱性。這項預測由楊振寧與李政道首先在1956年提出,隔年吳健雄便經由實驗證實了這項預測。楊振寧與李政道也因這項貢獻而獲得1957年的諾貝爾物理獎。再舉一個例子,塞曼效應的原子譜線分裂,因為外磁場所造成的微擾項目使得哈密頓量不再具有對稱性。
量子場論的重整化可能會造成對稱性破缺。例如,重整化會造成手征性異常(chiral anomaly),即違反強互動作用手征對稱性(chiral symmetry)的異常。
由於量子場論的不可重整效應,可能會出現對稱性破缺。現代場論的觀點認為所有理論都只是有效理論,只是所謂的終極理論的低能量近似。終極理論可能不遵守有效理論的拉格朗日量所具有的對稱性。這種對稱性又稱為“意外對稱性”。在高能量區域,意外對稱性可能會被打破。
1.在理論或實驗的基礎上,直接加入破壞對稱項目。最著名的例子,如量子場論中的弱互動作用破壞了宇稱的對稱性。這項預測由楊振寧與李政道首先在1956年提出,隔年吳健雄便經由實驗證實了這項預測。楊振寧與李政道也因這項貢獻而獲得1957年的諾貝爾物理獎。再舉一個例子,塞曼效應的原子譜線分裂,因為外磁場所造成的微擾項目使得哈密頓量不再具有對稱性。
2.量子場論的重整化可能會造成對稱性破缺。例如,重整化會造成手征性異常(chiral anomaly),即違反強互動作用手征對稱性(chiral symmetry)的異常。
3.由於量子場論的不可重整效應,可能會出現對稱性破缺。現代場論的觀點認為所有理論都只是有效理論,只是所謂的終極理論的低能量近似。終極理論可能不遵守有效理論的拉格朗日量所具有的對稱性。這種對稱性又稱為“意外對稱性”。在高能量區域,意外對稱性可能會被打破。
明顯對稱性破缺與自發對稱性破缺大不相同,後者的定義方程式滿足對稱性,但是系統的最低能量態(真空態)打破了這對稱性。
塞曼效應
1896年由荷蘭物理學家彼得·塞曼發現了處於外磁場的原子,其譜線的分裂現象,這稱為塞曼效應。
這原子的哈密頓量為
 明顯對稱性破缺
明顯對稱性破缺 明顯對稱性破缺
明顯對稱性破缺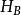 明顯對稱性破缺
明顯對稱性破缺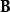 明顯對稱性破缺
明顯對稱性破缺其中,是原子的零微擾哈密頓量,是由外磁場造成的微擾。
這微擾的形式為
 明顯對稱性破缺
明顯對稱性破缺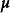 明顯對稱性破缺
明顯對稱性破缺其中,是原子的磁矩。
 明顯對稱性破缺
明顯對稱性破缺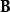 明顯對稱性破缺
明顯對稱性破缺這物理系統的具有空間對稱性(球對稱性或對於某平面的對稱性),但是外磁場設定了特別方向(例如,垂直於對稱平面),打破了對稱性,因此產生譜線的分裂現象。
參閱
•自發對稱性破缺
•手征對稱性破缺
