定義
定義一
在平面內,將一個圖形繞一點按某個方向轉動一個角度,這樣的運動叫做圖形的旋轉。這個定點叫做旋轉中心,轉動的角度叫做旋轉角。旋轉中各個旋轉角的大小相等。圖形的旋轉是圖形上的每一點在平面上繞著某個固定點旋轉固定角度的位置移動,其中對應點到旋轉中心的距離相等,對應線段的長度、對應角的大小相等,旋轉前後圖形的大小和形狀沒有改變。
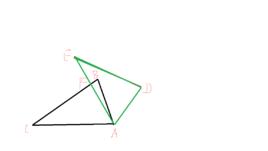
例如 AB線段繞A旋轉90度到AB、 旋轉角就是∠BAB、 度數是90度。
定義二
旋轉角是複變函數的導數的輻角的幾何意義。
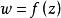 旋轉角
旋轉角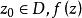 旋轉角
旋轉角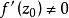 旋轉角
旋轉角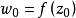 旋轉角
旋轉角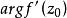 旋轉角
旋轉角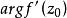 旋轉角
旋轉角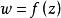 旋轉角
旋轉角設 在區域 D 內連續, 在 z 點有導數,則當經過 z 點的的任一曲線 L 在處切線與實軸之間的夾角恰好等於 L 在z處的切線與實軸之間的夾角與 之和,因而稱為映射在z點的旋轉角。
性質
經過旋轉,圖形上的每一點都繞旋轉中心沿相同方向轉動了相同的角度,任意一對對應點與旋轉中心的連線所成的角都是旋轉角,對應點到旋轉中心的距離相等。一個圖形和它經過旋轉所得的圖形中,對應點到旋轉中心的距離相等,任意一組對應點與旋轉中心的連線所成的角都等於旋轉角;對應線段相等,對應角相等。
圖形圖例
右圖,用五角星舉例子。黑色的五角星為原圖,將它旋轉72°後,與紅色三角形重合,
就稱為旋轉對稱,某一圖旋轉90°或180°後,與原圖重合,就為旋轉對稱圖形,那么旋轉的度數就為旋轉角(設角為α 0°<α<360°)。
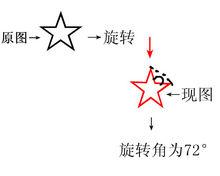 旋轉圖例
旋轉圖例