旋轉反伸軸

旋轉反伸軸是晶體中一根假想的直線，晶體圍繞此直線旋轉一定角度後，再對此直線上的個點進行反伸，可使晶體上相等的部分重複。其對稱操作是圍繞一根直線的旋轉和對此直線上一個點的反伸。

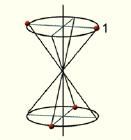
相應的幾何要素是一個假想的定點與通過此點的一根假想直線兩者的組合。當物體或圖形繞此直線旋轉一定的角度後,緊接著再藉助於此假想點的倒反(也可以先倒反再旋轉),其最後結果可使各相同部分發生重複。類似於對稱軸,旋轉反伸軸也有一定的軸次和基轉角,且同樣不能存在5次和高於6次的旋轉反伸軸。通常用符號Lin表示。晶體中可能存在的旋轉反伸軸及其符號如下表。旋轉反伸軸軸次(n)n=1,2,3,4,6基轉角(α)a=360°180°120°90°60°習慣符號(Lin)Li1、Li2、Li3、Li4、Li6。除了Li4之外，其餘各種旋轉反伸軸都可以用其他簡單的對稱要素（P對稱面、L對稱軸、C對稱中心）或它們的組合來代替，其關係是：Li1=C; Li2=P; Li3=L3+C; Li6=L3+p⊥。鑒於以上的代替關係，對旋轉反伸軸通常只保留Li4、Li6，其他旋轉反伸軸都用簡單對稱要素來代替。保留Li4是以為它不能被其他簡單對稱要素代替，保留Li6是因為它在晶體的對稱分類中有特殊意義。值得指出的是，在晶體或晶體模型上有Li4的地方往往表現出L2的特點，導致誤認為是L2。可以認為：L2是包含在L4中的。