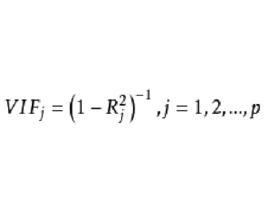基本介紹
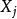方差擴大因子
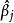方差擴大因子方差擴大(膨脹)因子法是通過考察給定的解釋變數被方程中其他所有解釋變數所解釋的程度，以此來判斷是否存在多重共線性的一種方法。方程中的每一個解釋變數都有一個方差擴大(膨脹)因子(variance inflation factor，VIF)，它反映的是多重共線性在多大程度上增大估計係數方差的指標。統計上可以證明，解釋變數、參數估計值的方差可表示為：
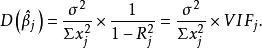方差擴大因子
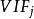方差擴大因子 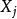方差擴大因子
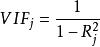方差擴大因子
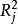方差擴大因子 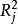方差擴大因子 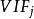方差擴大因子
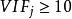方差擴大因子式中，是變數的方差擴大因子，即，這裡的是多個解釋變數輔助回歸的可決係數。越大，說明變數間多重共線性越嚴重，方差膨脹因子也就越大。經驗表明，時，說明解釋變數與其餘解釋變數之間有嚴重的多重共線性。且這種多重共線性可能會過度地影響最小二乘估計 。
在不存在多重共線性的情況下，方差擴大因子接近於1。但是，實際上自變數之間總是或多或少地存在多重共線性，因而將方差擴大因子等於1作為評價共線性的標準是不現實的。多重共線性越強，方差擴大因子就越大。一個易用的標準：當VIF值大於10時，就認為變數之間具有強烈的多重共線性，不能接受。
如果VIF暗示自變數之間存在過於強的相關性，那么可以採用的補救措施如下：
(1)去掉VIF較大的變數。
(2)將相關的變數組合成單一的一個變數。
多重共線性的診斷
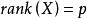方差擴大因子
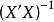方差擴大因子
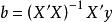方差擴大因子多元線性回歸模型的一個基本假設，就是要求自變數矩陣X的列滿秩，即秩(要求X中的列向量之間與線性無關)。如果X的列不滿秩，則將不存在，於是基於最小二乘的回歸係數估計，將不存在，所以很難得出穩定的結果。
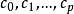方差擴大因子如果存在不全為0的p+1個數，使得:
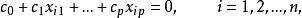方差擴大因子
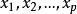方差擴大因子 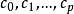方差擴大因子則自變數之間存在 完全多重共線性。實際問題中，當存在不全為0的p+1個數，使得:
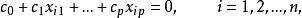方差擴大因子 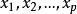方差擴大因子則稱自變數之間存在著 多重共線性，也稱為 復共線性。
考慮線性回歸模型：
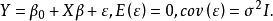方差擴大因子
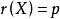方差擴大因子
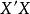方差擴大因子這裡假定X已中心標準化，且，這時即為相關陣R。下面給出幾個常用的復共線性診斷方法及其一般標準 。
完全多重共線性的情況並不多見，在回歸分析之前，也很容易發現存在完全多重共線性的解釋變數。可以採用以下三種方法來判斷是否存在完全多重共線性：第一，考察一個變數是否是另一個變數的倍數；第二，考察一個變數是否等於另一個變數加上一個常數項；第三，考察一個變數是否等於另外兩個變數相加。如果存在以上幾種情況，就應該剔除其中的一個變數。
方差擴大因子法
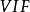方差擴大因子方差擴大因子()定義為：
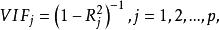方差擴大因子 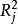方差擴大因子 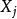方差擴大因子
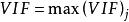方差擴大因子其中為對其餘p-1個自變數的復相關係數的平方，。
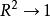方差擴大因子
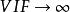方差擴大因子可以看出，當時。
一般標準：
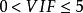方差擴大因子①當時，沒有復共線性；
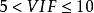方差擴大因子②當時，有較弱的復共線性；
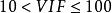方差擴大因子③當時，有中等或較強的復共線性；
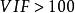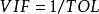方差擴大因子
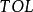方差擴大因子
方差擴大因子 方差擴大因子④當時，有嚴重的復共線性。由於(稱為容忍值)，所以也可以用來診斷復共線性。
在此僅討論VIF，有的統計軟體給出的是容忍值。
特徵根分析法
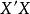方差擴大因子的p個次序特徵根為：
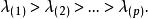方差擴大因子一般標準：
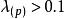方差擴大因子①當時，可認為不存在復共線性；
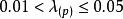方差擴大因子②當時，有弱的復共線性；
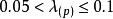方差擴大因子③當時，有中等或較強的復共線性；
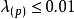方差擴大因子④當時，有嚴重的復共線性。
條件數法
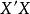方差擴大因子
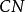方差擴大因子
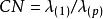方差擴大因子方陣的條件數()定義為：
一般標準：
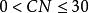方差擴大因子①當時，沒有復共線性；
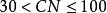方差擴大因子②當時，有較弱的復共線性；
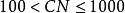方差擴大因子③當時，有中等或較強的復共線性；
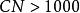方差擴大因子④當時，有嚴重的復共線性。
直觀判定法
當增加或剔除一個自變數，或者改變一個觀測值時，回歸係數的估計值會發生較大變化，我們就認為回歸方程存在嚴重的多重共線性。
從定性分析的角度來看，若一些重要的自變數在回歸方程中沒有通過顯著性檢驗，可初步判斷它們存在著嚴重的多重共線性。若自變數的回歸係數所帶正負號與定性分析結果違背，我們就認為它們存在著多重共線性問題；自變數的相關矩陣中，自變數間的相關係數較大時，可能會出現多重共線性；一些重要的自變數的回歸係數的標準誤差較大時，可能存在多重共線性 。
