簡介
【名稱】
Sgn
【類別】
數學函式
【原形】
Sgn(number)
【參數】
必選的,number 參數是一個 任何有效的數值表達式
【返回值】
如果 number 為
大於 0
1
等於 0
0
小於 0
-1
【異常/錯誤】
無
【描述】
返回一個 Variant (Integer),指出參數的正負號。number 參數的符號決定了 Sgn 函式的返回值。
【示例】
本示例使用 Sgn 函式來判斷某數的正負號。
Dim MyVar1, MyVar2, MyVar3, MySign
MyVar1 = 12: MyVar2 = -2.4: MyVar3 = 0
MySign = Sgn(MyVar1) ' 返回 1。
MySign = Sgn(MyVar2) ' 返回 -1。
MySign = Sgn(MyVar3) ' 返回 0。
【備註】
無
函式定義
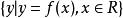 數學函式
數學函式函式是數學中的一種對應關係,是從非空數集A到實數集B的對應。簡單地說,甲隨著乙變,甲就是乙的函式。精確地說,設X是一個非空集合,Y是非空數集 ,f是個對應法則 , 若對X中的每個x,按對應法則f,使Y中存在唯一的一個元素y與之對應 , 就稱對應法則f是X上的一個函式,記作y=f(x),稱X為函式f(x)的定義域,集合為其值域(值域是Y的子集),x叫做自變數,y叫做因變數,習慣上也說y是x的函式。對應法則和定義域是函式的兩個要素。
函式相關概念
自變數,函式一個與他量有關聯的變數,這一量中的任何一值都能在他量中找到對應的固定值。
因變數(函式),隨著自變數的變化而變化,且僅當自變數取唯一值時,因變數(函式)有且只有唯一一值與其相對應。
幾何含義
函式與不等式和方程都存在著聯繫(初等函式)。令函式值等於零,從幾何角度看,對應的自變數是圖像與X軸交點;從代數角度看,對應的自變數是方程的解。另外,把函式的表達式(無表達式的函式除外)中的“=”換成“<”或“ >”,再把“Y”換成其它代數式,函式就變成了不等式,可以求自變數的範圍。
函式的集合論(關係)定義
 數學函式
數學函式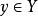 數學函式
數學函式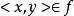 數學函式
數學函式如果X到Y的二元關係fÍX×Y,對於每個,都有唯一的,使得,則稱f為X到Y的函式,記做:f:X→Y。
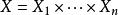 數學函式
數學函式當時,稱f為n元函式。
其特點:
前域和定義域重合;
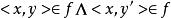 數學函式
數學函式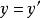 數學函式
數學函式單值性:→