分類
三維圖形平面投影
•平行投影：投影中心與投影平面的距離是無限的，投影線相互平行
•正投影（正交投影）：投影線垂直於投影平面
•多視圖投影：物體的坐標面與投影面平行，正視圖、側視圖、俯視圖
•軸測投影：物體的三個坐標面或坐標軸與投影面均不平行
•正等軸測投影（正等測）：投影時三個坐標軸等比例縮放，投影面坐標軸夾角120°
•正二軸測投影（正二測）：投影時兩個坐標軸等比例縮放，第三個坐標軸縮放比例不同
•正三軸測投影（正三測）：投影時三個坐標軸縮放比例均不相等
•斜投影：投影線不垂直於投影平面
•斜等軸測投影（斜等測）
•斜二軸測投影（斜二測）
•斜三軸測投影（斜三測）
•透視投影：投影中心與投影平面的距離是有限的
•一點透視
•兩點透視
•三點透視
平行投影
平行投影是投影線相互平行的投影。若投影線平行於投影面則稱正投影，若投影面傾斜於投影面則稱斜投影。
正交投影
正交投影是一系列用於顯示三維物體的輪廓、細節或精確測量結果的變換方法。通常又稱作截面圖、鳥瞰圖或立面圖。
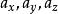數學三維投影
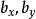數學三維投影當視平面的法向（即攝像機的朝向）平行於笛卡爾坐標系三根坐標軸中的一根，數學變換定義如下： 若使用一個平行於y軸（側視圖）的正交投影將三維點 投影到二維平面上得到二維點 ，可以使用如下公式
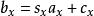數學三維投影
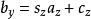數學三維投影其中向量 s是一個任意的縮放因子，而 c是一個任意的偏移量。這些常量可自由選擇，通常用於將視口調整到一個合適的位置。該投影變換同樣可以使用矩陣表示（為清晰起見引入臨時向量 d）
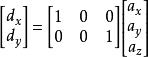數學三維投影
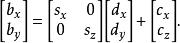數學三維投影雖然正交投影產生的圖像在一定程度上反映了物體的三維特性，但此類投影圖像和實際觀測到的並不相同。特別是對於相同長度的平行線段，無論離虛擬觀察者（攝像機）遠近與否，它們都會在正交投影中顯示為相同長度。這會導致較近的線段看起來被縮短了。
斜投影
斜投影不像正交投影一樣投影線垂直於投影面，而是投影線與投影面成非90度的斜角。
透視投影
透視投影的定義更為複雜。可以將其理解為透過攝像機取景器對於被投影物體進行觀察。攝像機的位置、朝向和視野都將影響投影變換的結果。我們定義以下變數來對這一變換進行描述：
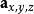數學三維投影1、：將被投影的三維空間中的點。
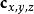數學三維投影2、：攝像機的位置。
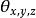數學三維投影
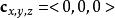數學三維投影
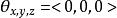數學三維投影3、：攝像機的旋轉角度。當且, 三維向量<1,2,0>將被投影到二維向量<1,2>。
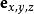數學三維投影4、：觀測者相對顯示平面的位置。
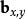數學三維投影
數學三維投影最終結果為：：所產生的二維投影。
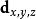數學三維投影 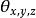數學三維投影
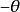數學三維投影首先我們定義點作為點 {\displaystyle \mathbf {a} } \mathbf {a} 向攝像機坐標系所作的變換，其中攝像機坐標系由攝像機的位置 c和旋轉所決定。該過程為：先用 a減去 c，然後使用由產生的旋轉矩陣乘上該結果。該變換通常稱為攝像機變換(注意該計算過程假設使用左手法則)：
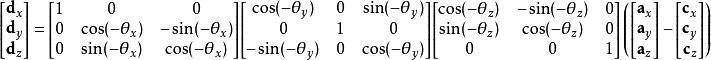數學三維投影或者使用以下這種非矩陣表示的形式，其中角度的正負號與矩陣表示形式不同：
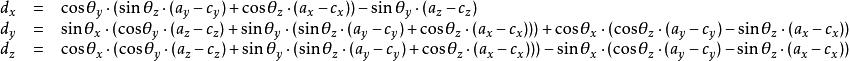數學三維投影然後將變換後的該點通過以下方程投影到二維平面（此處投影平面為 x/y平面，有時也使用 x/z）:
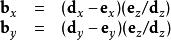數學三維投影或在齊次坐標系下可以表示為：
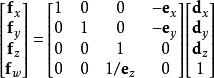數學三維投影和
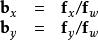數學三維投影
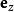數學三維投影
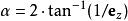數學三維投影觀測者到顯示平面的距離，，直接關係到視野的大小。為可視角度。（這裡假設螢幕的兩角為(-1,-1)和(1,1)）
如果要在一些特定的顯示設備上顯示該二維平面，之後還要進行一些必要的剪裁和縮放操作。
圖示
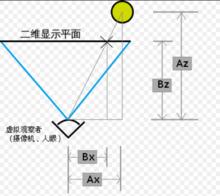數學三維投影計算三維空間中位於Ax，Az的點在螢幕坐標x軸的位置：
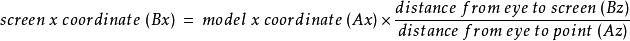數學三維投影對於y軸同樣有:
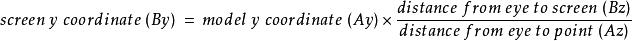數學三維投影(其中Ax和Ay是透視轉換前物體在空間中的坐標)
