數學思想
整體與部分的辯證。只有相對於部分所構成的整體而言,才是一個確定的部分,沒有整體,也無所謂部分。部分作為整體的組成,有時也可以當作一個整體。在數學上,從問題的整體性質出發,突出對問題的整體結構的分析和改造,發現問題的整體結構特徵,善於用“集成”的眼光,把某些式子或圖形看成一個整體,把握它們之間的關聯,進行有目的的、有意識的整體處理。所謂善於用“集成”的思想,譬如,太空梭有無數多的元器件組成,某個元器件發生故障,把該元器件所在的集成板整體換掉。
套用
有時給出的條件不是字母的具體值,就需要先進行化簡,求出字母的值,但有時很難求出字母的值或者根本就求不出字母的值,根據題目特點,將一個代數式的值整體代入,求值時方便又快捷,這種整體代入的技法經常用到。
例一、
若3a²-a-2=0,則 5+2a-6a²=
解析:由3a²-a-2=0,得-2=-3a²+a
等式兩邊都乘以2,得-4=-6a²+2a
把2a-6a² 看作一個整體等於-4整體代入5+2a-6a²=1
例二、
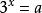 整體代入法
整體代入法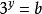 整體代入法
整體代入法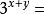 整體代入法
整體代入法已知,,那么
解析:看已知條件單求x,y 不容易。
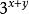 整體代入法
整體代入法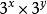 整體代入法
整體代入法在看,可以根據同底數冪的乘法的逆運算寫成,
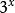 整體代入法
整體代入法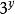 整體代入法
整體代入法把,分別看作一個整體,然後整體代入,得出a,b
