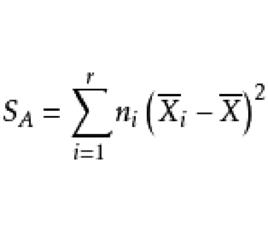基本介紹
總偏差平方和
在單因素方差分析(見下文)中,為了使造成各隨機變數X之間的差異的大小能定量表示出來,引入:
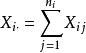 效應平方和
效應平方和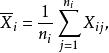 效應平方和
效應平方和記在水平A下樣本和為,其樣本均值為因素A下的所有水平的樣本總均值為
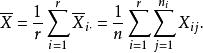 效應平方和
效應平方和為了通過分析對比產生樣本
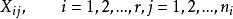 效應平方和
效應平方和之間差異性的原因,從而確定因素A的影響是否顯著,我們引人 偏差平方和來度量各個體間的差異程度
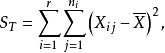 效應平方和
效應平方和因S能反映全部試驗數據之間的差異,所以又稱為 總偏差平方和。
誤差平方和與效應平方和
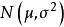 效應平方和
效應平方和如果H成立,則r個總體間無顯著差異,也就是說因素A對指標沒有顯著影響,所有的X可以認為來自同一個總體,各個X間的差異只是由隨機因素引起的,若H不成立,則在總偏差中,除隨機因素引起的差異外,還包括由因素A的不同水平的作用而產生的差異,如果不同水平作用產生的差異比隨機因素引起的差異大得多,就認為因素A對指標有顯著影響,否則,認為 無顯著影響。為此,可將總偏差中的這兩種差異分開,然後進行比較。
記
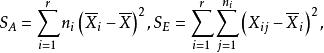 效應平方和
效應平方和則有下面的定理:
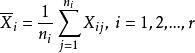 效應平方和
效應平方和定理1(平方和分解定理)令,有
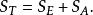 效應平方和
效應平方和S表示在水平A下樣本值與樣本均值之間的差異,它是由隨機誤差引起的,稱為 誤差平方和或 組內平方和。S反映在每個水平下的樣本均值與樣本總均值的差異,它是由因素A取不同水平引起的,稱為因素A的 效應平方和或 組間平方和,S=S+S式就是我們所需要的平方和分解式。
統計特性
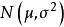 效應平方和
效應平方和如果H成立,則所有的X都服從常態分配,且相互獨立,則有:
定理2
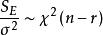 效應平方和
效應平方和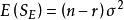 效應平方和
效應平方和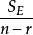 效應平方和
效應平方和(1),且,所以為σ 的無偏估計;
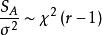 效應平方和
效應平方和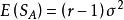 效應平方和
效應平方和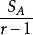 效應平方和
效應平方和(2),且,因此為σ 的無偏估計;
(3)S與S相互獨立;
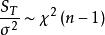 效應平方和
效應平方和(4)。
單因素方差分析
基本概念
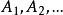 效應平方和
效應平方和在方差分析中,我們將要考察的對象的某種特徵稱為 試驗指標,影響試驗指標的條件稱為 因素,因素可分為兩類,一類是人們可以控制的(如原材料、設備、學歷、專業等因素);另一類人們無法摔制的(如員工素質與機遇等因素)。下面所討論的因素都是指 可控制因素。每個因素又有若干個狀態可供選擇,因素可供選擇的每個狀態稱為該因素的 水平。如果在一項試驗中只有一個因素在改變,則稱為 單因素試驗;如果多於一個因素在改變,則稱為 多因素試驗。因素常用大寫字母A,B,C,…來表示,因素A的水平用來表示,下面對單因素試驗進行討論。
假設前提
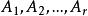 效應平方和
效應平方和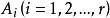 效應平方和
效應平方和設單因素A具有r個水平,分別記為,在每個水平下,要考察的指標可以看成一個總體,故有r個總體,並假設:
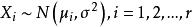 效應平方和
效應平方和(1)每個總體均服從常態分配,即;
(2)每個總體的方差σ 相同;
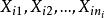 效應平方和
效應平方和(3)從每個總體中抽取的樣本相互獨立,i=1,2,…,r。
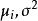 效應平方和
效應平方和此處的均未知,將假設及相關符號列表,如表1所示 。
| 水平 | 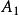 效應平方和 效應平方和 | 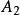 效應平方和 效應平方和 |  效應平方和 效應平方和 | 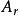 效應平方和 效應平方和 |
| 樣本 | 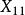 效應平方和 效應平方和 | 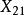 效應平方和 效應平方和 |  效應平方和 效應平方和 |  效應平方和 效應平方和 |
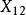 效應平方和 效應平方和 | 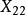 效應平方和 效應平方和 |  效應平方和 效應平方和 | 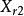 效應平方和 效應平方和 | |
 效應平方和 效應平方和 |  效應平方和 效應平方和 |  效應平方和 效應平方和 | ||
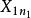 效應平方和 效應平方和 | 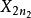 效應平方和 效應平方和 |  效應平方和 效應平方和 | 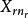 效應平方和 效應平方和 | |
| 樣本和 | 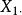 效應平方和 效應平方和 | 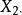 效應平方和 效應平方和 |  效應平方和 效應平方和 | 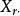 效應平方和 效應平方和 |
| 樣本均值 | 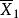 效應平方和 效應平方和 | 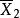 效應平方和 效應平方和 |  效應平方和 效應平方和 | 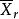 效應平方和 效應平方和 |
| 總體 | 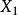 效應平方和 效應平方和 | 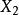 效應平方和 效應平方和 |  效應平方和 效應平方和 | 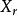 效應平方和 效應平方和 |
| 總體均值 | 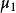 效應平方和 效應平方和 | 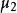 效應平方和 效應平方和 |  效應平方和 效應平方和 | 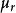 效應平方和 效應平方和 |
那么,要比較各個總體的均值是否一致,就是要檢驗各個總體的均值是否相等,設第i個總體的均值為μ,則
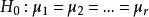 效應平方和
效應平方和假設檢驗為;
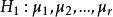 效應平方和
效應平方和備擇假設為不全相等。
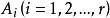 效應平方和
效應平方和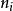 效應平方和
效應平方和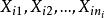 效應平方和
效應平方和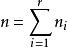 效應平方和
效應平方和在水平下,進行次獨立試驗,得到試驗數據,記數據的總個數為。
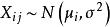 效應平方和
效應平方和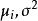 效應平方和
效應平方和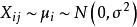 效應平方和
效應平方和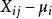 效應平方和
效應平方和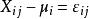 效應平方和
效應平方和由假設有(未知),即有,故可視為隨機誤差。記,從而得到如下數學模型:
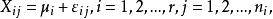 效應平方和
效應平方和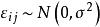 效應平方和
效應平方和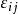 效應平方和
效應平方和 效應平方和
效應平方和,各個相互獨立,μ和未知。
方差分析的任務:
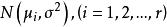 效應平方和
效應平方和(1)檢驗該模型中r個總體的均值是否相等;
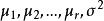 效應平方和
效應平方和(2)作為未知參數的估計。
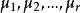 效應平方和
效應平方和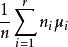 效應平方和
效應平方和為了更仔細地描述數據,常在方差分析中引入總平均和效應的概念,將各均值的加權平均值記為μ,即
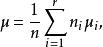 效應平方和
效應平方和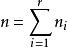 效應平方和
效應平方和其中再引入
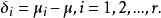 效應平方和
效應平方和δ表示在水平A下總體的均值μ與總平均μ的差異,稱其為因子A的第i個水平A的效應。易見,效應間有如下關係式
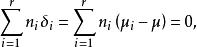 效應平方和
效應平方和利用上述記號,前述數學模型可改寫為
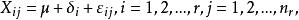 效應平方和
效應平方和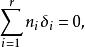 效應平方和
效應平方和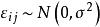 效應平方和
效應平方和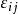 效應平方和
效應平方和 效應平方和
效應平方和,各個相互獨立,μ和未知。
而前述檢驗假設則等價於
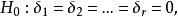 效應平方和
效應平方和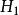 效應平方和
效應平方和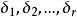 效應平方和
效應平方和:不全為零.
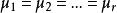 效應平方和
效應平方和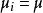 效應平方和
效應平方和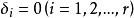 效應平方和
效應平方和這是因為若且唯若時,,即。