算法簡介
擴散算法是一種數據處理方法,目的在於通過擴散處理使得元素之間相互影響,從而實現完全的雪崩效應。雪崩效應是指原始輸入中的微小變化,經過積累發展後而造成輸出的巨大改變。而完全的雪崩效應,對於輸入中任意的微小變化都會造成輸出全部產生改變(100%的擴散率)。
擴散算法通過在元素之間建立擴散路徑,使元素沿著該路徑向其他元素擴散。每一個元素都沿著指定的路徑擴散,從而使元素間相互發生影響。
算法原理
擴散算法的核心在於擴散過程,擴散過程由擴散網路決定。所謂擴散,是指元素傳遞影響的過程,若元素A擴散到元素B,則當A發生改變時,B也發生改變。
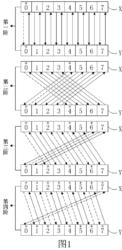 圖1(有序網路)
圖1(有序網路)若有N(N>=1)個元素組成的集合M。通過一定的規則使M中的元素相對應,如M(起點)對應M(終點),M對應M,M對應M,M對應M…,描述為M向M擴散,記作M→M;分別取出相對應的元素並組成表達式,通過一定的方法對表達式進行處理,再使用處理的結果更新被對應的元素(終點)。當起點元素髮生改變時,終點元素也發生改變;在處理的過程中這種改變會發生傳遞,進而影響其他元素,最終影響所有元素。
在上述過程中,元素間的對應關係用擴散路徑(以下簡稱路徑)表示,起點元素(M)叫做原體,終點元素(M)叫做受體;由元素組成的表達式叫做擴算式;對擴算式的處理叫做擴散運算(為防止受體丟失,擴散運算時需加入受體一同運算);所有路徑的集合叫做擴散網路(以下簡稱網路);對整個網路執行一次擴散叫做一個周期。
參照圖1,X、Y為元素數量均為8的分組;方框中的數字為元素索引,連線方框之間的線條為擴散路徑,箭頭指向的元素為受體元素,其中虛線表示元素X[0]完成完全擴散所走的路徑;元素索引上方的“*”號表示被X[0]所影響的元素;整個網路的擴散分為四個階段完成,執行擴散時需從上到下順序執行;
建立網路時,若要達到100%的擴散率,必須要保證所建立的網路對於每一個輸入元素都能影響任何一個輸出元素;每個擴散式的擴散運算都必須滿足原體中任意元素的變化都將引起受體的變化(受體為元素組時,則元素組內的每一個元素都要發生變化)。
算法特性
豐富的網路建立規則
 圖2(無序網路)
圖2(無序網路)網路可以建立為有序的(圖1),也可以建立為無序的(圖2)。
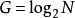 擴散算法
擴散算法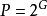 擴散算法
擴散算法對於有序的網路,則不需要手動建立路徑,直接套用公式即可。設N為分組長度,先計算對數 ,對G進行向上取整;計算基於N的完美長度 ;計算完成完全擴散所需的階段數量round=G+E, E>=0;E的取值範圍跟分組數量有關,E的具體取值可根據分組數量或者需要來設定。
對於無序的網路,則需要手動建立路徑,對於任意N長度的分組均存在最短路徑(即單位元素完成完全擴散所需的路徑長度,每一階為一個長度),或許可以通過算法找出該最短路徑,應該不是什麼難事;或許為了某種目的可以增加一些額外的路徑,讓網路看起來更加複雜。
豐富的擴散式建立方式
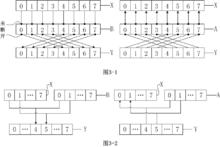 圖3(路徑連線方式之一)
圖3(路徑連線方式之一)擴散式的建立除必須包含原體和受體外,還可以包含其他任意元素(元素組),想怎么建,就怎么建了。
豐富的擴散運算方式
世間函式千千萬萬,誰人知道你用了誰。想從數據中分析出使用了什麼樣的函式,這幾乎是天方夜譚。只需稍稍更改一點函式參量,就能使數據變得面目全非,猶如蝴蝶扇翅而颶風忽起。
豐富的元素組織方式
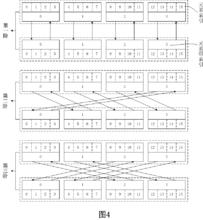 圖4(元素組擴散)
圖4(元素組擴散)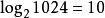 擴散算法
擴散算法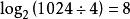 擴散算法
擴散算法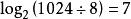 擴散算法
擴散算法完成完全擴散所需要的擴散階段跟元素數量有關,對於1024位元組長度的分組(元素類型為byte),則需要 個擴散階段。若將4個元素組成int類型,則只需要 個擴散階段。若將8個元素組成long類型,則僅需要 個擴散階段。當然,元素可以任意組合。不過使用組合元素也沒那么容易,這還需要滿足對於元素組內任意一個元素的變化都需要引起其他元素的變化(包括原體和受體)。元素組織方式可參見圖3。
天生的並行計算支持
每個擴散階段都需要對當前階段的每一條路徑進行擴散運算,因為目前的計算機以串列的方式執行指令,因此需要對這些路徑逐一執行擴散運算。但顯然這些路徑是可以一併執行的,不同路徑內的元素互不影響。如果每個階段的擴散運算都可以同一時刻並行處理的話,那么對於N個元素的擴散算法,理論上速度將提升N倍。
其他特性
簡潔,擴散算法真的只有那么簡單,區區幾行碼就可以達到那么不可思議的效果;靈活,如可以定製網路、定製擴散式、定製函式等。
算法用途
數據加密
擴散算法有著完美的擴散率,因此能夠很好的進行數據加密。而且加密過程非常簡單,天生的並行計算支持能夠極大提升加密速度。
可以將密匙作為分組一同建立路徑,或者將密匙作為擴散運算的參數一同參與運算。使用定製的函式並保密,可讓攻擊者不知所措。使用定製的網路並保密,將會使攻擊者感到異常頭疼。即便攻擊者知道網路建立規則,擴散式建立方式以及所使用的函式,那么也只能束手無策,唯一的攻擊方法就是窮舉攻擊。然而對於支持任意長度密匙的擴散加密,窮其所有,也只能望洋興嘆。當然密匙也不能太短了!
擴散算法其良好的擴展性,可有如下加密模式:
對稱分組加密:使用擴散算法進行加密,對每一組明文的加密都使用的相同的密匙(可以在每一階都使用不同的密匙)。
對稱流加密:僅使用擴散算法生成子密匙流(參見生成隨機數),再使用所生成的密匙流和明文進行異或運算(xor)即可得到密文。使用可靠的擴散運算(函式)再以消除線性,將使密匙重複變得遙遙無期。
對稱分組流加密:使用擴散算法以密匙為基礎生成子密匙流,再使用擴散算法對明文進行分組加密。此模式可以滿足對每一組明文的加密都使用不同的密匙。
半非對稱加密:套用擴散算法,可提高非對稱的加密效率。用非對稱加密數據時,不需要將整個明文組塊合成一個大整數進行加密,只需對明文中的各個元素(元素組)分別加密即可(密匙不同)。
此模式共分三次加密。設有明文M,長度為n;套用非對稱分別對M中的各個元素(M,M,M…M)進行加密後得到T;套用擴散算法對T進行加密後得到T;最後再次套用非對稱分別對T中的各個元素加密得到密文C(密匙與第一次加密相同)。
全非對稱加密:設函式F與函式Fˊ為非對稱互斥函式,通過F(Fˊ)加密後的數據只能通過F’(F)進行解密。套用擴散算法,在進行擴散運算的過程中使用F(Fˊ)進行加密,用Fˊ(F)進行解密即可。
計算訊息摘要
擴散算法可用於生成任意長度的訊息摘要。其100%的擴散率可計算出可靠的訊息摘要數據。對於其定製的擴散算法而言,在不泄露細節的情況下,碰撞攻擊幾乎變得毫無意義。
不過計算訊息摘要時,擴散運算的運算質量直接影響的到訊息摘要的計算質量,可不能馬虎。
生成MAC
MAC即訊息認證碼(帶密匙的訊息摘要)。這也不用說了,計算訊息摘要時加入密碼就好了。
生成偽隨機數
用擴散運算生成偽隨機數,隨機性好,生成速度快,周期長。使用可靠的函式是生成隨機數質量的前提保障,用多種網路交替使用更使隨機效果如虎添翼。可別忘了消除線性喔!
邏輯實現
有序網路
本示例的網路建立規則參照圖1。處理步驟:
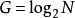 擴散算法
擴散算法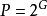 擴散算法
擴散算法S1. 設N(n)為分組長度。計算對數 ,並對G進行向上取整,計算完美長度 ,計算處理所需擴散階段的數量round = G + E,E>=1,本例E = 1。
S2. 取2組長度為n的分組X和Y,i、j分別是X、Y的元素索引。
S3. 設整數r是擴散階段索引號。第一階r = 0。由X向Y的擴散命名為E,記作E=X[i]+Y[j]→Y[j];由Y向X的擴散命名為E,記作E= Y[j]+X[i]→X[i]。組建擴散式分別為:
X[0]+Y[0]→Y[0], Y[0]+X[0]→X[0];
X[1]+Y[1]→Y[1], Y[1]+X[1]→X[1];
X[2]+Y[2]→Y[2], Y[2]+X[2]→X[2];
…
X[n-1]+Y[n-1]→Y[n-1], Y[n-1]+X[n-1]→X[n-1].
S4. 分別取出E中的原體,使用函式F計算結果後,更新E中的受體,即Y[j] = F(X[i], Y[j])。
S5. 分別取出E中的原體,使用函式F計算結果後,更新E中的受體,即X[i] = F(Y[j], X[i])。
S6. 第二階,r = 1。組建擴散式分別為:
X[0]+Y[P/2+0]→Y[P/2+0], Y[P/2+0]+X[0]→X[0];
X[1]+Y[P/2+1]→Y[P/2+1], Y[P/2+1]+X[1]→X[1];
X[2]+Y[P/2+2]→Y[P/2+2], Y[P/2+2]+X[2]→X[2];
…
X[n-1] +Y[P/2+n-1]→Y[P/2+n-1], Y[P/2+n-1] X[n-1]→X[n-1];
然後執行步驟S4、S5。
S7. 第三階,r = 2。組建擴散式分別為:
X[0]+Y[P/4+0]→Y[P/4+0], Y[P/4+0]+X[0]→X[0];
X[1]+Y[P/4+1]→Y[P/4+1], Y[P/4+1]+X[1]→X[1];
X[2]+Y[P/4+2]→Y[P/4+2], Y[P/4+2]+X[2]→X[2];
…
X[n-1] +Y[P/4+n-1]→Y[P/4+n-1], Y[P/4+n-1]+X[n-1]→X[n-1];
然後執行步驟S4、S5。
S8. 第r階(僅當此示例中不是第一階時)。組建擴散式分別為:
X[0]+Y[P/2 +0]→Y[P/2 +0], Y[P/2 +0]+X[0]→X[0];
X[1]+Y[P/2 +1]→Y[P/2 +1], Y[P/2 +1]+X[1]→X[1];
X[2]+Y[P/2 +2]→Y[P/2 +2], Y[P/2 +2]+X[2]→X[2];
…
X[n-1] +Y[P/2 +n-1]→Y[P/2 +n-1], Y[P/2 +n-1]+X[n-1]→X[n-1];
然後執行步驟S4、S5。
無序網路
本示例的網路建立規則參見圖2,處理步驟:
S1. 設有分組X、Y,分組長度為N,本例N=8。
S2. 計算處理所需擴散階段的數量round,round可根據網路建立規則和N進行調整,本例round 可取4。由X向Y的擴散記作E=X[i] +Y[j]→Y[j],由Y向X的擴散記作E=Y[j]+X[i]→X[i],i、j為元素索引。
S3. 第1階,組建擴散式分別為:
X[0]+Y[3]→Y[3], Y[3]+X[0]→X[0];
X[1]+Y[0]→Y[0], Y[0]+X[1]→X[1];
X[2]+Y[7]→Y[7], Y[7]+X[2]→X[2];
…
X[7]+Y[5]→Y[5], Y[5]+X[7]→X[7].
S4. 分別取出E中的原體,分別使用函式F計算結果後,更新E中受體的各元素,即:Y[j] = F(X[i], Y[j])。
S5. 分別取出E中的原體,分別使用函式F計算結果後,更新E中受體的各元素,即X[i] = F(X[i], Y[j]), 。
S6. 第2階,組建擴散式分別為:
X[0]+Y[5]→Y[5], Y[5]+X[0]→X[0];
X[1]+Y[3]→Y[3], Y[3]+X[1]→X[1];
X[2]+Y[4]→Y[4], Y[4]+X[2]→X[2];
…
X[7]+Y[1]→Y[1], Y[1]+X[7]→X[7];
然後執行S4、S5。
S7. 第3階,組建擴散式分別為:
X[0]+Y[2]→Y[2], Y[2]+X[0]→X[0];
X[1]+Y[4]→Y[4], Y[4]+X[1]→X[1];
X[2]+Y[0]→Y[0], Y[0]+X[2]→X[2]
…
X[7]+Y[3]→Y[3], Y[3]+X[7]→X[7];
然後執行S4、S5。
S6. 第4階,組建擴散式分別為:
X[0]+Y[0]→Y[0], Y[0]+X[0]→X[0];
X[1]+Y[1]→Y[1], Y[1]+X[1]→X[1];
X[2]+Y[2]→Y[2], Y[2]+X[2]→X[2];
…
X[7]+Y[7]→Y[7], Y[7]+X[7]→X[7];
然後執行S4、S5。
