擴散算法介紹
擴散算法是一種數據處理方法，目的在於通過擴散處理使得元素之間相互影響，從而實現完全的雪崩效應。雪崩效應是指原始輸入中的微小變化，經過積累發展後而造成輸出的巨大改變。而完全的雪崩效應，對於輸入中任意的微小變化都會造成輸出全部產生改變（100%的擴散率）。
擴散算法通過在元素之間建立擴散路徑，使元素沿著該路徑向其他元素擴散。每一個元素都沿著指定的路徑擴散，從而使元素間相互發生影響。
擴散算法的核心在於擴散過程，擴散過程由擴散網路決定。所謂擴散，是指元素傳遞影響的過程，若元素A擴散到元素B，則當A發生改變時，B也發生改變。
若有N（N>=1）個元素組成的集合M。通過一定的規則使M中的元素相對應，如M1（起點）對應M4（終點），M4對應M8，M8對應M2，M2對應M6…，描述為Mi向Mj擴散，記作Mi→Mj；分別取出相對應的元素並組成表達式，通過一定的方法對表達式進行處理，再使用處理的結果更新被對應的元素（終點）。當起點元素髮生改變時，終點元素也發生改變；在處理的過程中這種改變會發生傳遞，進而影響其他元素，最終影響所有元素。
在上述過程中，元素間的對應關係用擴散路徑（以下簡稱路徑）表示，起點元素（Mi）叫做原體，終點元素（Mj）叫做受體；由元素組成的表達式叫做擴算式；對擴算式的處理叫做擴散運算（為防止受體丟失，擴散運算時需加入受體一同運算）；所有路徑的集合叫做擴散網路（以下簡稱網路）；對整個網路執行一次擴散叫做一個周期。
建立網路時，若要達到100%的擴散率，必須要保證所建立的網路對於每一個輸入元素都能影響任何一個輸出元素；每個擴散式的擴散運算都必須滿足原體中任意元素的變化都將引起受體的變化（受體為元素組時，則元素組內的每一個元素都要發生變化）。
加密原理
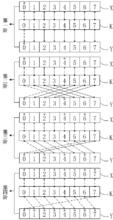圖1（有序的網路-加密/解密）擴散加密算法使用擴散算法 的原理進行加密/解密。擴散算法有著良好的擴展性，可加入任意數據一同參與處理。因此，將密匙作為參與處理的分組一同建立路徑，可是密匙具有多樣化的處理；使用各種各樣的函式進行擴散運算，可使同樣的加密變得豐富多樣。
參照圖1所示，X、Y為兩個明文分組，K為加密所用的密匙，各分組長度均為8，方框中的數字為元素索引；連線方框之間的線條叫做擴散路徑（以下簡稱路徑），X、Y到K的同一個元素上連線應表示為連通的（此處做了簡化才斷開顯示）。虛線表示X中第一個元素X[0]完成完全擴散所走的路徑；元素索引上方的“*”號表示被X[0]所影響的元素，因不更新K的元素，所以K的元素不發生改變（可按需要更新K的元素）；所有路徑的集合叫做擴散網路（以下簡稱網路）。整個擴散過程共分為4個擴散階段（擴散階段的數量與分組數量和分組內元素數量有關），執行擴散過程需按從上到下或者從下到上順序執行。
加密過程
參照圖1
第一步：建立擴散網路，將分組中的元素以某種規則建立網路（有序或無序）；所建立的網路必須滿足對於每一個輸入元素（X、Y、K）都能通過該網路擴散到任意一個輸出元素中（X、Y）。
第二步：以路徑為基礎建立擴散式，擴散式的建立是為確認參與擴散運算的元素。如：
X[0]+K[0]+Y[4]→Y[4],Y[4]+K[0]+X[0]→X[0];
X[0]+K[0]+Y[2]→Y[2],Y[2]+K[0]+X[0]→X[0];
X[0]+K[0]+Y[1]→Y[1],Y[1]+K[0]+X[0]→X[0];
......
建立擴散式時，擴散式除包含路徑所連線的元素之外，還可以包含其他任意元素。
第三步：對擴散式進行擴散運算，並使用運算的結果更新受體。為防止受體丟失，需加入受體一同運算。如
Y[4]=F(X[0], K[0], Y[4]), X[0] = F(X[0], K[0], Y[4])。函式F, F是可逆函式。
解密過程與加密相反。
算法特性
密匙長度任意
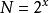擴散加密算法擴散算法支持任意長度、任意數量的分組進行處理，擴散加密算法同理。建議分組長度N滿足,x>=0且x為整數。擴散加密可以實現密匙和明文長度不等同，密匙即可以比明文短，也可以比明文長，具體可根據需要設定。
運算速度快
圖2（無序網路）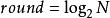
擴散加密算法擴散加密算法的核心代碼只有幾行，所使用的運算操作可以是速度極快的運算（如加法運算、異或（xor）運算、置換運算和移位運算），且只需少量的擴散階段即可完成明文塊的加密（設N為明文長度，則只需個擴散階段）。在每一階的擴散處理都可以使用並行處理，對於N長度的擴散處理，並行計算速度理論上比串列計算提高N倍。
擴散加密不需要顯式的對明文進行分組，可以直接對緩衝區進行（並行）處理，省去了明文的複製操作，進一步減少處理時間。
靈活的處理方式
網路可以建立為有序的（圖1），也可以建立為無序的（圖2）。相同長度的分組，有多種網路建立方案；豐富的擴散式建立方式，擴散式除包含路徑所連線的元素之外，還可以包含其他任意元素；豐富擴散運算方式，擴散運算可以使用任何函式進行運算（若需解密，則要求函式可逆）。
加密模式
擴散算法其良好的擴展性，可有如下加密模式：
對稱分組加密 ：使用擴散算法進行加密，對每一組明文的加密都使用的相同的密匙（可以在每一階都使用不同的密匙）。
對稱流加密：僅使用擴散算法生成子密匙流（參見生成隨機數），再使用所生成的密匙流和明文進行異或運算（xor）即可得到密文。使用可靠的擴散運算（函式）再以消除線性，將使密匙重複變得遙遙無期。
對稱分組流加密 ：使用擴散算法以密匙為基礎生成子密匙流，再使用擴散算法對明文進行分組加密。此模式可以滿足對每一組明文的加密都使用不同的密匙。
半非對稱加密：套用擴散算法，可提高非對稱的加密效率。用非對稱加密數據時，不需要將整個明文組塊合成一個大整數進行加密，只需對明文中的各個元素（元素組）分別加密即可（密匙不同）。
此模式共分三次加密。設有明文M，長度為n；套用非對稱分別對M中的各個元素（M1,M2,M3…Mn）進行加密後得到T1；套用擴散算法對T1進行加密後得到T2；最後再次套用非對稱分別對T2中的各個元素加密得到密文C（密匙與第一次加密相同）。
全非對稱加密：設函式F與函式Fˊ為非對稱互斥函式，通過F(Fˊ)加密後的數據只能通過F’(F)進行解密。套用擴散算法，在進行擴散運算的過程中使用F(Fˊ)進行加密，用Fˊ(F)進行解密即可。
