基本信息
自組織映射(Self-Organizing Maps, SOM)算法作為一種聚類和高維可視化的無監督學習算法, 是通過模擬人腦對信 號處理的特點而發展起來的一種人工神經網路。該模型由芬蘭赫爾辛基大學教授 Teuvo Kohonen 於 1981 年提出後,現在 已成為套用最廣泛的自組織神經網路方法,其中的 WTA(Winner Takes All)競爭機制反映了自組織學習最根本的特徵。
SOM算法是一種非監督(unsupervised)的聚類方法, 自20年前該算法提出至今很多研究者圍繞該算法在模式識別信號處理, 數據挖掘等理論和套用領域做了大量工作, 並且取得了大量研究成果。這些成果的取得很大程度上歸功於SOM算法本身的簡明性和實用性。
基本原理
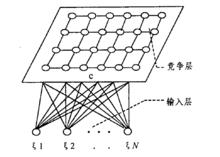SOM網路的典型拓撲結構SOM網路結構如圖 1 所示,它由輸入層和競爭層(輸出層)組成。輸入層神經元數為 n,競爭層由m 個神經元組成的一維或者二維平面陣列,網路是全連線的,即每個輸入結點都同所有的輸出結點相連線。
SOM 網路能將任意維輸入模式在輸出層映射成一維或二維圖形,並保持其拓撲結構不變;網路通過對輸入模式的 反覆學習可以使權重向量空間與輸入模式的機率分布趨於一 致,即機率保持性。網路的競爭層各神經元競爭對輸入模式 的回響機會,獲勝神經元有關的各權重朝著更有利於它競爭 的方向調整“即以獲勝神經元為圓心,對近鄰的神經元表現 出興奮性側反饋,而對遠鄰的神經元表現出抑制性側反饋, 近鄰者相互激勵,遠鄰者相互抑制”。一般而言,近鄰是指從 發出信號的神經元為圓心,半徑約為 50μm~500μm 左右的神經元;遠鄰是指半徑為 200μm~2mm 左右的神經元。比遠鄰更遠的神經元則表現弱激勵作用,如圖2所示由於這種交 互作用的曲線類似於墨西哥人帶的帽子,因此也稱這種互動方式為“墨西哥帽”。
神經元互動模式
SOM算法記所有輸出神經元c組成的集合為 ，神經元c與輸入層神經元之間的連線權向量為Wc。SOM算法作為一種非監督類的方法，理論上可以將人以為的輸入模式在輸出層映射成一維、二維甚至更高維的離散圖形，並保持其拓撲結構不變。
該算法的聚類功能主要是通過以下兩個簡單的規則實現的。
SOM算法 SOM算法1.對於提供給對於提供給網路的任一個輸入向量, 確定相應的輸出層獲勝神經元s，其中s=argminc| -Wc|所有的c屬於 。
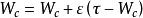SOM算法2.確定獲勝神經元 s 的一個鄰域範圍, 按如下公式調整，範圍內神經元的權向量：。該調整過程使得內神經元的權向量朝著輸入向量的方向靠攏。 所有的c屬於N。
SOM算法隨著學習的不斷進行,學習率 將不斷減小. 鄰域也將不斷縮小, 所有權向量將在輸入向量空間相互分離 , 各自代表輸入空間的一類模式,這就是Koohenn網路特徵自動識別的聚類功能。
具體過程
(1)將權值 賦予小的隨機初始值;設定一個較大的初始鄰域,並設定網路的循環次數 T;
SOM網路結構(2)給出一個新的輸入模式 Xk:Xk={X1k,X2k,...,Xnk},輸入到網路上;
(3)計算模式 Xk 和所有的輸出神經元的距離 djk,並選擇 和 Xk 距離最小的神經元 c,即
xk-Wc=minj{ dij }則 c 即為獲勝神經元;(4)更新結點 c 及其領域結點的連線權值 wij(t+1)=wij(t)+η(t)(xi-wij(t))
其中 0 <η(t)<1 為增益函式,隨著時間逐漸減小;
(5)選取另一個學習模式提供給網路的輸入層,返回步驟 (3),直到輸入模式全部提供給網路;
(6)令 t=t+l,返回步驟(2),直至 t=T 為止。
在自組織映射模型的學習中,通常取 500≤T≤10000。Nc 隨著學習次數的增加逐漸減小。增益函式 η(t)也即是學習率。 由於學習率 η(t)隨時間的增加而漸漸趨向零,因此,保證了學習過程必然是收斂的。
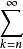SOM算法一般要求:η(t+k)=∞
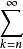SOM算法η^2(t+k)<∞
其中:0<η(t+k)<1,k=1,2,...,∞。
在實際的權係數自組織過程中,一般,對於連續系統取: η ( t ) = 1t
對於離散系統,則取:η(t+k)= 1/t+k
局限性
無導師學習現在發展的還不成熟,SOM 算法還存在一些局限性,比如:
(1)網路結構是固定的,不能動態改變;
(2)網路訓練時,有些神經元始終不能獲勝,成為“死神經元”;
(3)SOM 網路在沒有經過完整的重新學習之前,不能加入新的
類別;
(4)當輸入數據較少時,訓練的結果通常依賴於樣本的輸入順序; (5)網路連線權的初始狀態、算法中的參數選擇對網路的收斂性
能有較大影響。 為此,一些學者提出了不同的改進算法,從不同方面不同程度地克服了這些缺點。
SOM 的改進算法
基於動態確定神經元數目的改進
傳統 SOM 模型存在著許多的不足,特別是需要預先給定網路單元數目及其結構形狀的限制。為此,人們提出了多種在訓練過程中動態確定網路形狀和單元數目的解決方案, 比較有代表性的有: GSOM(Growing Self-Organizing network ))。該算法的基本思想是把n維 空間的單形體, 比如一維空間的線段, 二維空間的三角形, 三維空間的四面體作為基本的構建模組, 隨著訓練的不斷進行，漸進、動態地生成SO M網路。
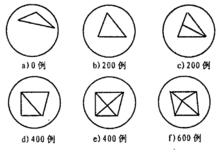
右圖就是將Growing SOM算法套用於一個圓形機率分布的數據集上所得到的最初幾步結果。
由上例可以看出, 隨著學習過程的不斷進行。SOM網路也在不斷“增長” ,平
Growing SOM套用與圓形機率分布的數據均每隔200個訓練例就有新的單形體(上例為三角形)插入到SOM網路中，那么這些單形體應該在什麼位置插入就成 G rowing SOM算法所面臨的一個關鍵問題, 一般而言,可以通過下述方法解決：對於整個SOM網路定義一個可以度量的期望目標；對於每一個輸出神經元(比如上例中的三角形的頂點)，估計它們對網路期望目標貢獻的大小；在那些對期望目標貢獻不大的神經元附近插入新的神經元；Growing SOM與普通的SOM網路的不同點在於：網路結構是動態生成的；持續不變的自適應能力；固定的鄰域範圍。相同點在於：固定的網路維數；鄰域的確定取決於網路的拓撲結構。
王莉等提出的樹型動態增長模型 TGSOM,它與 GSOM 的不同在於它可以按 需要方便地在任意合適位置生成新結點,克服了 GSOM 的缺 點;Frltzke 提出了增長細胞結構 (Growing Cell Structure, GCS)算法,GCS 算法從一個由 3 個神經元構成的三角形 結構開始,記錄下每個神經元獲勝的次數,在下一周期開始 前,選出獲勝次數最多的神經元,在其最大的一邊上增加一 個含初始權值的新結點,並重新計算新結點及各鄰接結點的 獲勝次數,同時,可根據結點的獲勝次數進行結點的刪除操 作。Choi 等提出了自組織、自創造的神經網路模型 (Self-creating and Organizing Neural Networks,SCONN), SCONN 在初始時存在一個激活水平足夠高的根結點,找出 輸入向量 x 的最佳匹配單元 c,然後比較|x - Wc|與 c的激活水平。若前者大於後者,生成一個 c 的子結點以匹配 x;否則, 修正 c 及鄰域結點的權值。
基於匹配神經元策略的改進
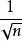SOM算法
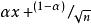SOM算法Kohonen 競爭學習機制經常會使得競爭層中有些結點始 終不能獲勝,儘管 SOM 採用拓撲結構來克服此缺點,但並不是非常有效,為此提出了很多克服此缺點的算法,比較典型的 有 : SOFM-CV , SOFM-C , ESOM(Expanding Self- organizing Map),TASOM(Time Adaptive SOM),DSOM。 SOFM-CV 的思想是:把 SOM 網路的權值都初始化為 ( n為輸入向量的維數),每個輸入向量 x 要經過如下修正後: ( (α 隨時間從 0 逐漸增大),再輸入網路。SOFM-C 即帶“良心”的競爭學習 SOFM,它的基本思想是給每個競 爭層結點設定一個閾值,每次使競爭獲勝的神經元的閾值增 加,使經常獲勝的神經元獲勝的機會減小。ESOM 的思想是 把更新獲勝結點 c 及其領域結點的權值公式(2)修改為下式: wij(t+1)=cj(t)(wij(t)+η(t)(xi-wij(t)))
其中 cj(t)≥1,由 wij(t),xi,η(t)確定。在 TASOM 中,每個神經 元都有自己的學習率和鄰域函式,並且能根據學習時間自動 地調整學習率和鄰域的大小。DSOM 的思想是把內源性一氧 化氮(NO) 的四維動態擴散特性和其在長時間學習過程中的 增強作用套用到 SOM 中,輸入向量 x 輸入網路後,以某種 規則(評價函式)確定競爭層中一組獲勝神經元,稱為亞興奮 神經元簇。並把每一個亞興奮神經元作為 NO 的擴散源。然 後計算各亞興奮神經元所處位置的 NO 濃度, 則 NO 濃度最 高的神經元為最終獲勝單元。
SOM 算法和其它算法的組合
比較有代表性的組合算法有:Xiao 等提出了把 SOM和微粒群最佳化(Particle swarm optimization,PSO)算法結合用來 對基因數據進行聚類,先用 SOM 算法對基因數據進行聚 類,得到一組權值,然後用此權值初始化 PSO 算法,用 PSO 算法對此聚類結果進行最佳化。Sankar 等提出了把粗糙集和 SOM 結合的 RSOM 算法,它先用粗糙集理論中的依賴規則 獲得輸入數據的大致聚類情況等知識,然後通過這些知識來 確定 SOM 網路的結構,並對 SOM 權值進行初始化,用 SOM 網路對結果進行訓練、最佳化。Hussin 等提出了把 SOM 和自 適應共振理論 (Adaptive Resonance Theory,ART)模型相結合 用來對文檔進行聚類,先用 SOM 算法對文檔進行劃分, 然後用 ART 對所有的劃分進行聚類。孫放等提出了把 SOM 和多層感知器(Multilayer Perceptron, MLP)結合進行語音識 別,首先用 SOM 算法進行語音特徵矢量量化(VQ),用軌 跡圖訓練 MLP 網路,相當於建立好了參數模板,用此參數 模板就可以進行語音識別。
SOM變體
TS-SOM
TS-SOM(Tree Struetured Self一Organzing Maps)是SOM算法的一種快速實現。TS-SOM的網路結構可以用一個圖T=(V,El,E2)來表示,其中V是結點(神經元)的集合,E1是用於“縱向”層次連線的邊構成的集合, 而E2是用於各層之間“ 橫向” 連線的邊構成的集合。 對於每一個節點i屬於V,都存在一個相應的子樹Ti(Vi,E1i,E2i),並且滿足如下條件：Vi屬於V，E1i屬於E1,E2i屬於E2，Ti與Tj不相交。
一維及二維的TS-SOM圖是一維和二維的TS-SOM的拓撲結構。在TS-SOM中,樹的每一層都是一個SOM網路,並且每一個結點都會引導出2^n個子結點,其中n為TS一SOM的維數,由此可知TS-SOM的第l層包含(2^n)^l個結點(l=0,1,2...L-1,L為TS-SOM的層數)。
由於樹結構本身的遞歸性 在對第l層上的神經元進行匹配運算時, 可以利用前面l-1層網路所提供的信息以減少匹配次數J.H.Friedman等人指出,對於總共含有N個結點的網路和任一輸入模式,普通SOM網路需要O(N)的時間以找出對應的獲勝神經元,而TS-SOM只需O(logpN)的時間就可以完成匹配, 其中戶是TS-SOM中每個神經元子結點的數目,且P=2^n。因此TS-SOM實際上是將樹結構有效地套用於SOM算法當中給出了SOM算法的一種快速實現 。
SOM 的套用
SOM 算法以其所具有的諸如拓撲結構保持、機率分布保持、無導師學習及可視化等特性吸引了廣泛的注意,各種關於SOM 算法套用研究的成果不斷湧現,現已被廣泛套用於 語音識別、圖像處理、分類聚類、組合最佳化(如 TSP 問題)、 數據分析和預測等眾多信息處理領域。總之,SOM 算法的 套用十分廣泛,有著較好的發展前景,值得大家作進一步的研究。
