擴散係數
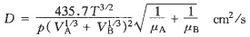 菲克定律
菲克定律物質的分子擴散係數表示它的擴散能力,是物質的物理性質之一。根據菲克定律,擴散係數是沿擴散方向,在單位時間每單位濃度梯度的條件下,垂直通過單位面積所擴散某物質的質量或摩爾數,即
可以看出,質量擴散係數D和動量擴散係數ν及熱量擴散係數α具有相同的單位(m/s)或(cm/s),擴散係數的大小主要取決於擴散物質和擴散介質的種類及其溫度和壓力。質擴散係數一般要由實驗測定。某些氣體與氣體之間和氣體在液體中擴散係數的典型值如表2-1所示。
 擴散係數D
擴散係數D其中,液相質擴散,如氣體吸收,溶劑革取以及蒸餾操作等的D比氣相質擴散的D低一個數量級以上,這是由於液體中分子間的作用力強烈地束縛了分子活動的自由程,分子移動的自由度縮小的緣故。
二元混合氣體作為理想氣體用分子動力理論可以得出D~p-1T的關係。不同物質之間的分子擴散係數是通過實驗來測定的。表2-2列舉了在壓強p=1.013×105Pa、溫度T=273K時各種氣體在空氣中的擴散係數D,在其它p、T狀態下的擴散係數可用下式換算
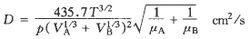 換算
換算兩種氣體A與B之間的分子擴散係數可用吉利蘭(Gilliland)提出的半經驗公式估算
(2-22)
式中,T:熱力學溫度,K;p:總壓強,Pa;μA、μB:氣體A、B的分子量;VA、VB:氣體A、B在正常沸點時液態克摩爾容積,cm3/gmol。幾種常見氣體的液態克摩爾容積可以查表2-3。
 表2-3
表2-3按式(2-22),擴散係數D與氣體的濃度無直接關係,它隨氣體溫度的升高及總壓強的下降而加大。這可以用氣體的分子運動論來解釋。隨著氣體溫度升高,氣體分子的平均運動動能增大,故擴散加快,而隨著氣體壓強的升高,分子間的平均自由行程減小,故擴散就減弱。當然,按狀態方程,濃度與壓力、溫度是相互關聯的,所以質擴散係數與濃度是有關的,就象導熱係數與溫度有關一樣。式(2-22)中D的單位是cm2/s,它和動量擴散係數ν=μ/ρ以及熱擴散係數α=λ/cpρ的單位相同,在計算質擴散通量或摩爾擴散通量時,D的單位要換算為m2/s。
分子擴散傳質不只是在氣相和液相內進行,同樣可在固相記憶體在,如滲碳煉鋼、材料的提純等等。在固相中的質擴散係數比在液相中還將低大約一個數量級,這可用分子力場對過程的影響更大,使分子移動的自由度更小作為合理的定性解釋。
二元混合液體的擴散係數以及氣-固、液-固之間的擴散係數,比氣之間的擴散係數要複雜得多,只有用實驗來確定。
分類
簡介
擴散係數可分為自擴散係數、互擴散係數及內擴散係數。
銅(Cu)及金(Au)在Al中的擴散係數
條件:448K(175℃)
Cu: 0.092×10^19[m^2/s]
Au: 3.9×10^19[m^2/s]
(注:半導體行業中接合點可靠性分析過程中需要考量的數據。)
液體擴散係數
相對粘度,它的物理意義是溶液粘度與純溶劑粘度的比值:ηr=η/η0。相對粘度是整個溶液的行為
。
斯托克斯-愛因斯坦(Stocks-Einstein)方程是解釋粘度與擴散係數之間關係的,D*VIS=kT/6*PI*R。假設粒子半徑為R的剛球質點A在稀溶液B中擴散。這裡面存在兩個基本假設:1,球形(SPHERE),2,剛性體,這樣運動基元的擴散運動就可以看成是獨立的、與溶劑分子不相關(uncorrelated)的個體行為。SE方程的失效往往是由於這兩個基本假設的失效:1,分子非球形,2,擴散基元與溶液分子存在耦合。前者的改變產生的影響有可能相對小一些。SE方程在溫度遠高於熔點的溫度區間沒問題,因為在高溫區間,溶液中的分子可以看成無關聯的,這時候溶液中基元的弛豫基本上是純指數的。但是,最近大量的實驗結果表明(例如剛剛出來的PRL文章),當溫度低於一定的臨界值,SE方程開始失效。至於這一臨界溫度,目前沒有一個定論,有人認為可能是一個稱為TA的溫度(對於大多數液體在這個溫度下液體弛豫時間可能達到10_-7秒左右),也有最近PRL文章認為在高於液相溫度幾百度的溫度上。無論如何,SE方程的失效都是由於溶液中原子或分子之間存在著關聯,從而運動有可能變為COOPERATIVE或者COLLECTIVE的方式
。
氣體擴散係數
揮發性液體之氣體擴散係數可藉由Winklemann’s method來檢測,在有限內徑的垂直毛細管中保持固定的溫度和經過毛細管頂部的空氣流量,可確定液體表面的分子擴散到氣體中的蒸氣分壓)
。
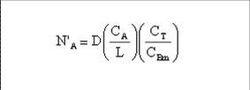 公式
公式已知質傳速率:
D = 擴散速率 (m2/s); CA= A物質於界面間的飽和濃度 (kmol/m3);L =質傳有效距離(mm);CBm=蒸氣的對數平均莫耳濃度 (kmol/m3);CT = 總莫耳濃度=CA+CBm (kmol/m3)
