概念
擬正規族(quasi-normal family)是正規族概念的一種推廣。在擬正規族的定義中不要求子序列f(z)(k=1,2,…)在D的內部一致收斂,而只要求除去D內有窮個點(或無窮個點但在D內沒有凝聚點),在所余的區域內部一致收斂。
正規族
正規族是具有某種收斂性質的函式族。定義如下:在一個區域D的一個全純函式族F稱為在D內為正規,如果從F的每一個函式序列f(z)(n=1,2,…)都可以選出一個子序列f(z)(k=1,2,…),使得它在D的內部一致收斂到一個全純函式或一致發散到∞。
一個全純函式族F在一個區域D內為正規的一個充分條件都稱為正規性定則。蒙泰爾(Montel,P.A.)指出:如果F是區域D內一致有界的全純函式族,則F是正規族.經過進一步的研究,蒙泰爾證明了“F中的函式在D內均不取二固定的有窮值a及b”是一個正規性定則。由蒙泰爾的這個重要的正規性定則,很容易推出皮卡的小定理及大定理,由它還很容易推出肖特基定理及蘭道定理。為了說明蒙泰爾的這個正規性定則的另一個套用,先引進下列定義:設F為在一區域D的一個全純函式族並考慮D內一點z,如果存在一個以z為中心的圓C,使在C內F為正規,則稱F在z為正規。顯然,如果F在D內為正規,那么,F在D內每點為正規。反過來,如果F在D內每一點為正規,那么F在D為正規。因此,假定已知F在D為不正規,那么至少存在D內一點z,使F在z不正規,這樣的點z稱為一茹利亞點。根據最後這個事實及上述蒙泰爾的正規性定則,茹利亞(Julia,G.M.)證明了下列定理:如果f(z)是一個超越整函式,那么,最少存在一條茹利亞方向。
正規族的理論有廣泛的套用,它是蒙泰爾於1912年引進的.蒙泰爾引進正規族的概念之後,又進一步引進了擬正規族的概念。利用正規族和擬正規族兩個概念,蒙泰爾推廣了維塔利(Vitali,G.)的一個定理。經過卡拉西奧多里(Carathéodory,C.)、蘭道(Landau,E.G.H.)、蒙泰爾及奧斯特洛夫斯基(Ostrowski,A.M.)的工作,亞純函式正規族理論也已建立起來.如果一致收斂性是用球面距離來定義,那么,亞純函式的正規族的定義如下:在一個區域D的一個亞純函式族F稱為在D內為正規,如果從F的每一函式序列f(z)(n=1,2,…),都可以選出一個子序列f(z)(k=1,2,…)在D的內部一致收斂。關於亞純函式族蒙泰爾的正規性定則是:F中的函式在D內均不取三個固定的值a,b及c(有窮或無窮).類似地可給出亞純函式擬正規族的定義。
全純函式正規族及亞純函式正規族理論已經發展到了完善的地步。這個理論中的一個重要研究課題是尋求新的正規性定則,在這方面,布洛赫(Bloch,A.)的下列猜測很有指導意義:如果p是一個性質,非常數的整函式(或非常數的亞純函式)不具有性質p,那么,在一個區域內具有性質p的全純函式族(或亞純函式族)是正規的。這個猜測在一些例子中都是對的,例如與關於整函式的劉維爾(Lioville,J.)定理相應的是以上蒙泰爾的關於一致有界的全純函式族的定理,與關於整函式的皮卡定理相應的是以上蒙泰爾的關於有兩個有窮例外值的全純函式族的定則。
收斂
當無窮級數、無窮序列或無窮乘積的極限存在,就稱為收斂或具有收斂性。
例如,對於一個數a及數列{a},如果對任意的ε>0,都存在一個正整數N,使得當n>N時,都有丨a-a丨<ε,就稱數列{an}以a為極限,或稱數列{an}收斂於a。
考慮無窮數列1/2,3/4,7/8,15/16,…;直觀地,它收斂於(或趨向於)極限1,這可以用精確的語言作如下表述: 不管數k是如何的大,總能找到相應的數m,使得該數列從第m項之後的任何項與1相差都小於1/k。如果存在某數使一個數列趨向於它,就說這個數列收斂。不收斂的數列可以是振盪的 (例如1,0,1,0,…)或者是發散的(趨向於無窮)(例如1,2,3,4,…)。把上述的定義對應到無窮級數的場合,那么,下列三個級數: 1/2+1/4+1/8+1/16+…,1-1+1-1+…,1+1+1+1+…,就顯然地對應於上述的三個數列。在微積分學和數學表的計算中,無窮級數都是有用的工具。
一致收斂
一致收斂亦稱均勻收斂。無窮級數的基本概念之一。它有兩種最基本的情形:
1.函式列的一致收斂。若函式f和所有的f(n=1,2,…)都在集合A(R)上有定義,任給ε>0,存在正整數N,使得當n>N時,對於所有的x∈A,有|f(x)-f(x)|<ε,則稱函式列{f(x)}在A上(關於x)一致收斂於函式f(x),並將f(x)稱為{f(x)}的一致極限(函式)。這個定義也可改述為:若
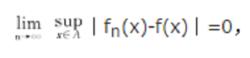 擬正規族
擬正規族則稱f(x)在A上一致收斂於f(x)。
2.多元函式關於它的一部分自變數的一致收斂.以二元函式f(x,y)在集合B(R)上當x→x時關於y一致收斂於φ(y)的概念為例,首先要求f在A×B上定義(即當x∈A,y∈B時,有相應的函式值f(x,y)),φ在B上定義,x是A的聚點.若對任給的ε>0,存在與y無關的δ>0,使得只要|x-x|<δ時,就有|f(x,y)-φ(y)|<ε對一切y∈B成立,或者說,若有
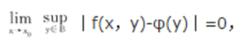 擬正規族
擬正規族則f(x,y)稱為(在B上,當x→x時)關於y一致收斂於φ(y)。
由以上兩種情形的定義出發,稍加變化即可得到其他各種情形下一致收斂的定義。例如,函式項級數∑f(x)的一致收斂,指其部分和函式序列{S(x)}一致收斂;二元函式f(x,y)關於x當y→+∞時一致收斂的定義為:對任意ε>0,存在M>0,使得只要y>M,就對一切x∈E有|f(x,y)-φ(x)|<ε;含參量廣義積分
 擬正規族
擬正規族一致收斂於F(x)可敘述為:若令
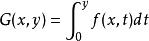 擬正規族
擬正規族而G(x,y)當y→+∞時,關於x一致收斂於F(x),則稱
 擬正規族
擬正規族關於x一致收斂。有關一致收斂的判別法及性質,以函式列情形為主簡介如下,其他情形是類似的。常用判別一致收斂的準則及判別法有:柯西準則,M判別法,狄利克雷判別法,阿貝爾判別法與迪尼定理。若函式列{f(x)}關於x在[a,b]上一致收斂於f(x),則當每個f在x∈[a,b]連續時,f在x也連續;當每個f在[a,b]上可積,f在[a,b]也可積,且
 擬正規族
擬正規族若每個f在[a,b]上可微,且{f′(x)}(f的導函式序列)關於x在[a,b]上一致收斂,且{f}在某點收斂,則{f(x)}一致收斂於某個可微函式f(x)(在[a,b]上),且
 擬正規族
擬正規族在函式列和函式項級數情形下,後兩條相當於逐項積分和逐項微分。一致收斂的概念是外爾斯特拉斯(Weierstrass,K.(T.W.))於19世紀50年代末明確,由海涅(Heine,H.E.)於1870年建立的。
