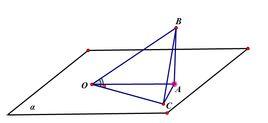
證明
 摺疊角公式
摺疊角公式如圖,可知AB⊥平面α,取OC上一點C使得∠OCA=90°,即CA⊥OC
根據三垂線定理可得BC⊥OC
在Rt△BOA中
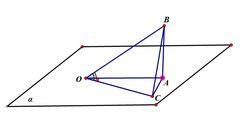
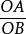 摺疊角公式
摺疊角公式cos∠AOB= ①
在Rt△COA中
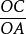 摺疊角公式
摺疊角公式cos∠AOC= ②
在Rt△COB中
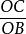 摺疊角公式
摺疊角公式cos∠COB= ③
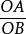 摺疊角公式
摺疊角公式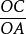 摺疊角公式
摺疊角公式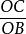 摺疊角公式
摺疊角公式比較①、②、③三式可知 x =
即得證cos∠BOC=cos∠AOBcos∠AOC
例題使用
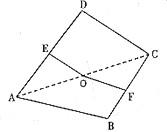 摺疊角公式
摺疊角公式如圖,點O是正方形紙片ABCD的中心,點E,F分別為AD,BC的中點,現沿對角線AC把紙片折成直二面角,則紙片折後∠EOF的大小為?
考點:摺疊角公式的套用
專題:計算題(摺疊角公式的套用)
分析 :過過F作FG垂直於AC,G在AC上,連線GE,由摺疊角公式可得cos∠EOF=cos∠FOG·cos∠GOE,根據正方形的性質及等腰直角三角形的性質,我們易得∠AOF=135°,∠AOE=45°,進而我們可以求出∠EOF的餘弦值,進而得到∠EOF的大小.
解答:解:過F作FG垂直於AC,G在AC上,連線GE;
∵二面角B-AC-D為直二面角,
∴FG⊥平面ACD(直二面角的性質),
∵FO為平面ADC的斜線,OE在平面ADC內,
由摺疊角公式得:cos∠EOF=cos∠FOG·cos∠AOE…(1)
∵∠FOG=180°-∠AOF,∠GOE=180°-∠AOE(鄰補角定義),代入(1)得:
cos∠EOF=(-cos∠AOF)·(-cos∠AOE),
即cos∠EOF=cos∠AOF×cos∠AOE.
由∠AOF=135°,∠AOE=45°
∴cos∠EOF=cos135°·cos45°=-0.5
則∠EOF=120°
點評:本題考查的知識點是與二面角有關的立體幾何綜合題,其中過F作FG垂直於AC,為摺疊角公式的使用創造條件,是解答本題的關鍵.
註明:摺疊角公式以及三正弦定理的套用為立體幾何的解題帶來了許多方便。
公式特點
輔助記憶:這三個角中,∠COB是最大的,其餘弦值最小,等於另外兩個角的餘弦值之積。斜線與平面所成∠AOB是斜線與平面內所有直線所成的角中最小的角。
(運用時可以背誦成,橫的角乘以豎的角等於斜的角)
推論一
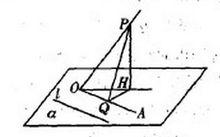 摺疊角公式
摺疊角公式PO是平面α的一條斜線,PH⊥α,垂足為H,l為平面α內任意一條直線
(與OH的射影不重合也不平行),設PO與直線l所成角為θ,PO與平
面α所成角為θ1,OH與直線l所成較小角為θ2,則cosθ=cosθ2cosθ2
推論二
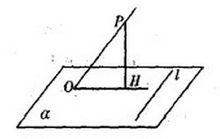 摺疊角公式
摺疊角公式摺疊角公式(三餘弦定理)逆定理依舊成立
推論三
從空間一點O引出的三條射線OA、OB、OC滿足
 摺疊角公式
摺疊角公式 摺疊角公式
摺疊角公式 摺疊角公式
摺疊角公式 摺疊角公式
摺疊角公式∠AOC=∠AOB×∠BOC,則面AOB⊥面BOC