術語簡介
任何物理可實現電路,在換路瞬間電路中的儲能不發生突變.
由於電容通過電場儲能,能量公式為 0.5×C×sqrt(U)
所以在0+和0-這兩個時間點的U必然是相等的,也即U不能突變(能量不能突變)。
 換路定理
換路定理同理,電感通過磁場儲能,能量公式為 0.5×L×sqrt(I),所以在0+和0-這兩個時間點的I必然是相等的,也即I不能突變(能量不能突變)。
對於電容,U(0+)=U(0-),對於電感,I(0+)=I(0-)。就是換路定理的核心。
定理分析
由動態元件組成的動態電路有一個重要的特徵即:當電路的結構或元件的參數發生突然改變時(例如電路中電源的斷開或接入、無源元件的斷開或接入、元件參數的突然變化、信號的突然改變或置零等等),將會使電路改變原來的工作狀態,轉變到另外一種工作狀態,這種情況稱為“換路”, 而這種變化往往是和能量的變化連在一起的,而能量的變化是需要經歷一個過程的,在工程上稱為“過渡過程” 。
 換路定理
換路定理在求解“過渡過程”的變數時,必須有一個初始值的計算,例如動態元件中的電容元件(又稱為儲能元件),如果電路中僅含一個電容元件,該電路就稱為一階動態電路。
分析一階動態電路的過渡過程方法之一仍然是根據KCL,KVL 和支路VCR 來建立描述電路的方程,該方程是以時間為自變數的線性微分方程,這種方法又稱為經典法, 是一種在時間領域中分析的方法。
用經典法求解微分方程時,必須根據電路的初始條件確定解中的積分常數,而初始條件就是指電路中所求變數及其(n - 1)階導數在t =0 +時的值, 這個值就稱為初始值。
電容電壓uC(0 +)稱為獨立的初始條件。
適用範圍
(1) 如果電路中存在有全部由電容元件組成的迴路或由電容元件與理想電壓源組成的迴路,當激勵接入或者換路時,電容電壓可能發生躍變 。
 換路定理
換路定理(2)如果電路中存在有全部由含電感元件組成的割集或由含電感元件與理想電流源組成的割集,當激勵接入或電路發生換路時,電感電流也可能發生躍變。
在電路發生“強迫躍變”的情況下,只能根據電荷守恆和磁鏈守恆的原理確定狀態變數有關的初始值, 這時如果仍然按照“換路定理”進行分析與計算就是錯誤的。
與基爾霍夫定律的關係
 換路定理
換路定理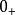 換路定理
換路定理 換路定理
換路定理 換路定理
換路定理換路定理與基爾霍夫定律的關係換路定理的基本定義是”在換路前(t= )和換路後(t= ),線圈的磁鏈不變[ ],電容的電荷不變[ ]"。
 換路定理
換路定理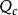 換路定理
換路定理 換路定理
換路定理 換路定理
換路定理因為如果 或 突變,則或就會變成無窮大,這在電壓源的電路中就要違背KVL,在電流源的電路中就要違背KCL。
 換路定理
換路定理線上性(恆定參量)電路中,線圈的電感量L,電容的容量C 均為常數,這時因為。, 便引伸出常用的衍定理,即:
 換路定理
換路定理 換路定理
換路定理在換路前後,,。
必須強調,衍定理的正確是有附帶條件的, 即換路時原元件的參量L(或C) 不變。

