簡介
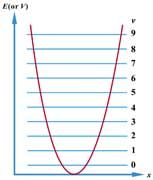諧振子勢能曲線和能級圖分子振動能級間隔較大，約為0.05-leV.振動躍遷通常伴有轉動躍遷，稱為振-轉光譜，每一條振動譜帶中包含若干條轉動譜線.液態和固態樣品中分子間作用較強,或者由於儀器記錄範圍較寬、解析度較低，往往分辨不出振動譜帶中的轉動譜線，一個譜帶就呈現為一個峰.分子中有多種振動躍遷，整個分子的振動光譜包含若干條譜帶.
分子振動可能引起分子固有偶極矩的變化，也可能引起分子極化率的變化.這兩種變化可以分別產生紅外光譜和拉曼光譜.其中,紅外吸收位於近紅外和中紅外區.
雙原子分子的紅外光譜
諧振子模型:對於雙原子分子的振動,也有一種簡化處理——諧振子模型.
設雙原子分子的兩個原子核在平衡距離re(即鍵長)附近往復振動,回復力服從虎克定律,由此可以寫出勢能V的算符,與動能T的算符一起構成總能量的哈密頓算符,進而寫出Schrodinger方程:
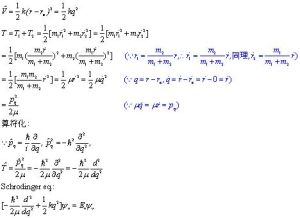方程
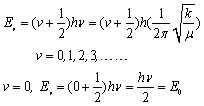振動能級振動量子數v=0的能量就是零點能E0，這是一種量子效應,說明分子即使在無限接近0K時振動也不停息.這是測不準原理的一種表現.
諧振子能級是振動量子數v的一次函式，故振動能級是等間隔的，間隔為hv.
諧振子振動躍遷選律
振動躍遷也受整體選律和具體選律的限制.
整體選律：只有能夠引起分子固有偶極矩變化的振動方式才可能觀察到紅外光譜.這對多原子分子也是適用的.極性分子的固有偶極矩在分子骨架振動過程中總會發生變化,所以,極性分子總有紅外光譜.但是,能不能反過來說,非極性分子一定沒有紅外光譜呢?只有對非極性的雙原子分子才能這樣說,因為它們只有一種不改變分子固有偶極矩變化的伸縮振動.但不能說非極性的多原子分子也一定沒有振動光譜.N個原子組成的分子共有3N-6種簡正振動方式(直線形分子有3N-5種),每一種簡正振動是否可能具有紅外活性,應由整體選律來考察(這與任何非極性分子都沒有轉動光譜是不同的).
例如,苯是12個原子組成的非極性分子,它有30種簡正振動方式,其中有許多種能夠引起分子固有偶極矩變化,可觀察到紅外光譜.但有一些振動方式就沒有紅外活性，例如，有一種“呼吸振動”就沒有紅外活性，因為這種振動不會引起分子固有偶極矩變化.
具體選律：才有Δv=±1的躍遷是允許的.
諧振子能級是等間隔的，間隔為hv.再考慮到具體選律只允許Δv=±1的躍遷,可以得出結論:即使分子分布在多種振動能級上,它們躍遷時也都對應著相同的能量吸收,因而只有一個振動峰(若考慮其中包含的多條轉動譜線,就是一條譜帶).實際上,振動能級間隔較大,室溫下大部分分子處於振動基態,因而主要是v=0到v=1的躍遷.
實驗表明這一推斷基本是正確的,確實只有一條很強的基本譜帶;但推斷又不完全正確,因為還發現了一些波數近似等於基本譜帶整數倍而強度迅速衰減的泛音譜帶.這一現象表明諧振子模型有缺陷.
不難想像,分子不可能是完全的諧振子,而應當是非諧振子.因為諧振子的拋物形勢能曲線暗示著:分子的核間距無論拉到多長,化學鍵也不會被破壞.至少這一點肯定是不真實的.所以,讓我們再看看非諧振子模型.
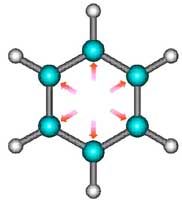苯分子的“呼吸振動”
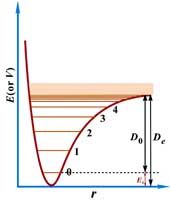非諧振子勢能曲線和能級圖 (D0=De-E0)非諧振子模型:對於非諧振子模型提出過幾種勢能函式,例如
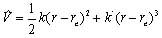公式由此建立振動方程，解出的振動能級不再等間隔：
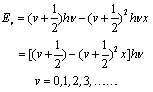公式式中x為非諧性係數.
非諧振子的整體選律與諧振子相同,但具體選律卻允許Δv=±1,±2,±3,……的躍遷.
考慮到室溫下大部分分子處於v=0的振動基態,可導出從v=0躍遷到任一高能級v的吸收波數公式,很好地解釋了實驗上觀察到的基本譜帶和泛音譜帶:
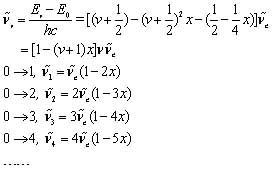公式其中,從v=0躍遷到v=1是基本譜帶,而v=0躍遷到v=2、3、4、…分別是第一、第二、第三、…泛音帶.
注意:
(1)由於此處低能級的振動量子數已指定為0,所以,這裡的波數公式都是以高能級的振動量子數v標記的,這不同於多數情況下用較低能級量子數作為下標的習慣;
(2)由於非諧振子振動波數公式中包含著諧振子振動波數,這裡將非諧振子和諧振子振動波數分別加下標v和e區分.
振轉光譜
振動激發可以同時伴隨轉動激發，用高解析度紅外光譜儀可觀察到振轉光譜.例如,HCl的振轉光譜如下:
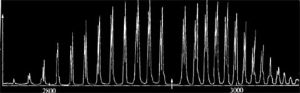HCl的振轉光譜左側譜帶波數較小,稱為P支;右側譜帶波數較大,稱為R支.它們都包含一組間隔為2B的譜線.中間位置本來有一條稱為Q支的譜帶,但對於Σ電子態,Q支是禁阻的,所以觀察不到.轉動譜線為雙重線是因為樣品中含25%的H37Cl,產生了向低波數方向的同位素位移.
用振轉能級圖結合躍遷選律,很容易解釋振轉譜帶是如何產生的：當振動激發同時伴隨轉動激發時，若高振動態的轉動量子數比低振動態的轉動量子數小1,產生波數較小的P支;若高振動態的轉動量子數比低振動態的轉動量子數大1,產生波數較大的R支.
注意:P支與R支都是針對譜帶位置而言,至於ΔJ=-1或+1,則由吸收或發射而定.通常教科書中說P支和R支分別由ΔJ=-1和+1的轉動譜線組成,這隻對吸收光譜才成立.當然,分子光譜主要使用吸收光譜.
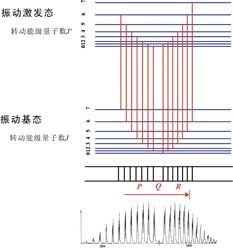HCl振轉能級圖與振轉譜帶示意圖多原子分子紅外光譜
N原子分子有3N個自由度,其中有3個屬於平動,3個屬於轉動(直線形分子為2個),剩餘的3N-6個為振動自由度.每個振動自由度有一種稱之為正則振動或簡正振動的運動方式:所有原子以同頻率、同位相振動，同時通過平衡點、同時到達極大值.正則振動方式可以用群論的方法處理,由投影算符給出.每種正則振動方式有一個特徵頻率,並可從理論上計算出來.
多原子分子的振動非常複雜.原則上,任何複雜振動都可以分解為正則振動的疊加,實際上,多原子分子的振動光譜很少直接使用純粹的理論計算來解析,而多用經驗規律解析.但近年來,計算化學中光譜模擬軟體發展很快,對於光譜的輔助解析作用值得重視.
一般說來,化學鍵的伸縮振動頻率大於彎曲振動頻率,重鍵振動頻率大於單鍵振動頻率,連線較輕的原子(如H)的化學鍵振動頻率較高.
頻率較高的振動不易受其它因素影響,能保留自己的特徵.經驗表明,官能團具有相對穩定的特徵頻率,因此,儘管任何振動方式原則上都是所有原子參與,但同一種官能團的振動頻率在不同化合物中大致相同,據此可以鑑別不同類型的化合物.
頻率較低的振動則很容易隨環境而變,特徵性很差,分子結構的細微差別就能引起這種振動的變化,因此反映的是每一種具體分子的結構信息,猶如人的指紋，這種振動出現的區域也就稱為“指紋區”.
IR譜的掃描範圍通常在4000-650cm-1,特徵頻率與指紋區大致以1500cm-1為界:
（1）特徵頻率區4000~1500cm-1,又可分成兩個小區:波數較高一端是與氫原子相結合的官能團，如OH、NH、CH鍵伸縮振動吸收帶（C-H、N-H、O-H，~3000cm-1）;波數較低一端是叄鍵、雙鍵和累積雙鍵如C=C=C的吸收帶（叄鍵~2100cm-1；雙鍵，1600-1700cm-1）.
（2）指紋區1500-650cm-1：這是單鍵伸縮振動和彎曲振動吸收（單鍵C-C、C-N、C-O，800-900cm-1）.
解析紅外光譜時可以查閱光譜手冊,其中有詳盡的特徵頻率表；若樣品已被研究過，則可通過索引查閱各種圖譜集，或查網上資料庫來對照.一般說來，紅外光譜完全相同的物質是同一種物質，只有對映異構體和少數大分子同系物是例外.
解析紅外光譜的基本步驟
紅外光譜對鑑別官能團、測定分子結構具有重要作用，但解釋複雜分子的紅外光譜並不容易，除了懂得基本原理外，更需要比較豐富的實踐經驗.初學者可以選擇一些比較簡單的分子作為練習，但不要急於很快取得成功.
(1)根據化合物的分子式寫出各種可能的結構式.
(2)按照特徵頻率表，對整個光譜圖認真檢查,看看有哪些官能團和骨架的特徵峰，如N-H、O-H、C=O、烯基、芳環等.
(3)檢查C-H伸縮區域(2700-3300cm-1)，辨別是否有不飽和或芳香環：
飽和烴的C-H伸縮一般不超過3000cm-1；
烯烴的C-H伸縮有對稱與反對稱之分:前者在2975cm-1處,往往與飽和烴甲基反對稱伸縮重疊;後者在3080cm-1處,是烯烴的特徵，但應注意芳烴C-H、鹵代烷、小環環烷的C-H伸縮也在此區；
芳烴的C-H伸縮在3030cm-1附近；
再檢查1360-1380cm-1區域，看是否有-CH2-和-CH3.
(4)若化合物除C、H、O外，還有其它原子X，則尋找X-H或X-C特徵峰.例如，亞胺的N=C伸縮振動峰在1690-1640cm-1區間，可判別亞胺基是否存在；而含有叄鍵的氰基C≡N伸縮振動峰在2245cm-1附近，若發生共軛則降低約30cm-1.
(5)若化合物不是芳香化合物，則725cm-1附近的寬頻表示四個以上的-CH2-基組成的長鏈.
(6)繼續查找其它特點.例如，單核芳烴的C=C伸縮振動在1500和1600cm-1附近有兩個峰,一般前者較強後者較弱,可作為芳核存在的標誌，等等.
紅外光譜儀
紅外光譜儀的光源可用碳化矽棒通過電熱發光.樣品池和稜鏡等用透紅外線的材料(如NaCI、KBr、LiF等)製作,也可用光柵分光.熱電偶或熱敏電阻探測器將訊號傳送給放大記錄系統.
付里葉變換紅外光譜簡介
傅立葉變換紅外光譜儀是非色散型光譜儀,其核心部分是一台雙光束干涉儀（常用邁克耳孫干涉儀）.當動鏡移動時,經過干涉儀的兩束相干光的光程差改變，到達探測器的光強隨之改變,得到干涉圖，再經傅立葉變換得到光譜.
傅立葉變換光譜儀的主要優點是:多道測量提高了信噪比;沒有入射、出射狹縫限制，光通量高使儀器靈敏度提高;以氦、氖雷射波長為標準,波數值精確度可達0.01cm-1;增加動鏡移動距離可提高解析度;工作波段從可見區可延伸到毫米區,實現遠紅外光譜測定.
拉曼光譜
分子振動也可能引起分子極化率的變化，產生拉曼光譜.拉曼光譜不是觀察光的吸收,而是觀察光的非彈性散射,因此光源的頻率不必與振動躍遷對應的頻率相一致,例如用可見或紫外光源照射在樣品上，在垂直於入射光的方向，觀測散射光的強度隨波長的變化關係，非彈性散射峰頻率和彈性散射峰頻率(即入射光頻率)之差反映出分子的振動轉動能級.非彈性散射光很弱，故拉曼光譜過去較難觀測.雷射拉曼光譜的出現使靈敏度和分辨力大大提高，套用日益廣泛.
拉曼現象可以在各種入射光頻率下發生(例如用波長為632.8nm的He-Ne雷射).拉曼光譜由於產生機理和紅外光譜不同,在選律方面也不相同.
光子與分子碰撞時,少部分在側向散射.其中,又有大部分是頻率不變的彈性散射,少部分是頻率增大或減小的非彈性散射.頻率增減是由於非彈性散射時光子與分子交換能量引起的,頻率減小和增大分別產生Stokes線與反Stokes線.
對於有對稱中心的分子,任何一種振動方式都不會在紅外與拉曼光譜上都觀察到,稱為互斥規則.研究分子結構時二者可以互補.根據群論知識容易明白：光譜強度與下列矩陣元平方成正比.為保證矩陣元不為零，被積函式的宇稱必須為g.紅外光譜的躍遷矩算符為u宇稱的偶極矩算符,而拉曼光譜的躍遷矩算符為G宇稱的極化率算符.由於大多數分子的始態ψi為g宇稱，所以，躍遷的終態ψj在紅外與拉曼光譜上的宇稱必須分別是u和g:
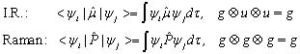公式沒有對稱中心的分子不存在互斥規則.
