純振動躍遷
 圖1
圖1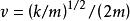 振動躍遷
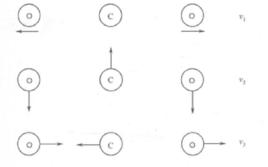
振動躍遷作為一級近似,可用諧振子模型描述雙原子分子的振動。一個簡單的諧振子是一個力學體系,它由點質量m和無質量彈簧所組成。作用在此質量上的恢復力與質點從其平衡位置的位移及彈簧的力常數k成正比。勢能V與此位移的平方成正比,振動頻率v則由式 給出。
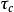 振動躍遷
振動躍遷 振動躍遷
振動躍遷同樣,對於雙原子分子,V是原子核間距r從其平衡位置 的位移q(或折合質量為 真的粒子從重心的位移)的函式。此勢能函式呈拋物線形,如方程12-4所示(此處討論的所有方程見圖1)。在Schrodinger方程中,用這一勢能函式得到的結果是方程(12-5)所描述的量子化能級。在光譜的中或遠紅外區可觀察到振動吸收躍遷。
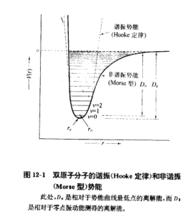 圖2
圖2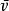 振動躍遷
振動躍遷僅在接近平衡核間距時,實際的振動勢能才能非常好地符合拋物線函式。對於所有的間距,表示在方程(12-8)中的Morse勢能函式才能更接近地符合分子振動的勢能。這一函式的形狀及所觀察到的雙原子分子的振動能級顯示在圖2中。若在Schrodinger方程中用Morse勢能函式,則解會更複雜。方程(12-9)是由非諧振子模型得到的能級近似解,方程(12-9)中第二項導致在接近分子解離限的大小v值處可觀察到能級的收斂性。諧振子模型預期所有能級都按 等距離分布,且允許鍵斷裂。
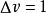 振動躍遷
振動躍遷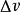 振動躍遷
振動躍遷振動能級間躍遷選律為 ,此外,必須發生偶極矩變化,以致在1R吸收光譜中同核雙原子分子並不顯示振動躍遷。有時可觀察到叫做泛頻的弱躍遷,這些躍遷對應於 =2或3。
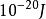 振動躍遷
振動躍遷振動能級的通常能量間隔大約為 。由Boltzmann分布可以看出,不存在外部輻射時,在室溫下處於激發態的分子通常為1%或更少。因此在室溫下,觀察到最多的吸收躍遷是從v=0能級到v=1能級。
CO2的振動躍遷
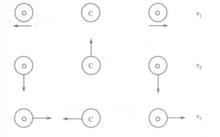 圖3
圖3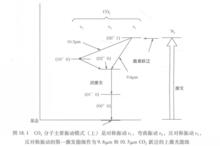 圖4
圖4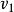 振動躍遷
振動躍遷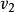 振動躍遷
振動躍遷 振動躍遷
振動躍遷圖3表示CO分子的三種主要振動模式:對稱振動模式 ;彎曲模式口 ;反對稱振動模式 。如圖4所示,每種振動模式有其本身的量子化能級分布。這些模式中,彎曲模式的能級最小,對稱振動模式能級約為彎曲模式的兩倍,反對稱振動模式的能級則更大。
這些振動能級中成對能級問的躍遷形成振動雷射器。和四能級電子躍遷雷射器一樣,外部能量源使反轉粒子增加到泵浦能級。分子迅速從泵浦能級衰退到長壽命亞穩態,處於上雷射能級,然後激發輻刺使分子降低至下雷射能級,最後衰退至基態。所有的四個能級都是基態電子能級中的振動能級。
振動躍遷對應於1~100μm的紅外波長,因此比電子躍遷需要較少的激勵能量。但需要注意的是每個振動能級伴隨數十種轉動能級。量子力學的法則要求當分子從一個振動能級運動到另一振動能級時,需要精確的改變一個轉動能級。想一想這個要求的含義,如果分子開始於上振動能級的第三轉動能級,其必須終止於下振動能級的第二或第四轉動能級;如果其開始於第六轉動能級,其必須終止於第五或第七轉動能級,結果是每個振動躍遷包含可能的轉動躍遷。所有的努力使振動雷射器發射出一個較寬範圍的波長,對應振動躍遷加上(或減去)轉動躍遷的能量。
CO雷射是上述工作模式的典型代表。如圖4所示,首先被激勵的CO的反對稱振動是兩雷射躍遷的上雷射能級。如果受激發的分子衰退至對稱振動的第一激發態,其釋放一個名義波長10.5μm的光子。或者,它衰退至轉動模式的第二激發能級,釋放9.6μm的光子。10.5μm的躍遷較強,但是雷射器可以同時在兩個波長上振盪。
 圖5
圖5如圖5所示,每種振動躍遷有其自身的一族轉動躍遷。距離振動躍遷名義中心的每個間隔對應轉動能量的一個能級間隔。CO雷射可以同時在一條或者多條譜線上振盪取決於諧振腔鏡。為能量傳輸設計的工業用雷射器運行在較寬頻寬上,其名義波長為10.6μm,但實際出射光線在9~11μm之間。科學研究用雷射器和某些有特殊用途的雷射器通常將振盪限制在頻寬的一小部分或者一個單一的轉動譜線上。
轉動-振動躍遷
 圖6
圖6在高解析度情況下觀察氣態雙原子分子的振動光譜時可發現,每一個譜帶都含有大量距離靠得很近的組分。由於這一點,分子光譜常叫做帶光譜。根據振動躍遷期間轉動的激發可解釋觀察到的結構,這種振動轉動光譜的形狀可由振動一轉動分子的能級預測。對簡單的雙原子分子且不用非諧性和離心校正的情況下,方程(12一10,見圖1)給出了以波數為單位時可能發生的躍遷的能量。
由v到v+1的振動吸收躍遷可產生三組稱作支的譜線,如圖6所示。較低頻率的P支對應於△v=1和△J=-1的躍遷,而Q支對應於△v=1和△J=0的躍遷。而較高頻率的Q支對應△v=1和△J=+1的躍遷,除了具有奇數個電子的雙原子分子(例如NO)除外,對雙原子分子觀察不到Q支。在吸收光譜中,R和P帶中各組分的相對強度則由振動基態中各轉動能級的布居和簡併度所決定。