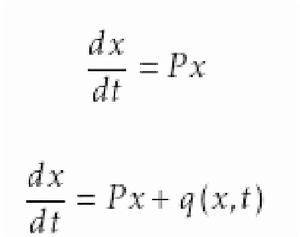基本介紹
對於常係數線性方程組
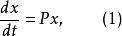按一次近似決定穩定性其解的漸近性態是很清楚的。如果在(1)的右端加上一個小擾動，即
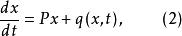按一次近似決定穩定性則人們試圖從(1)的解的已知性態去獲得(2)在原點附近的漸近性態，這就是通常所稱的 按一次近似決定穩定性的問題 。
相關結論
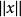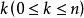按一次近似決定穩定性
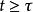按一次近似決定穩定性
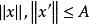按一次近似決定穩定性
按一次近似決定穩定性
按一次近似決定穩定性當P沒有零或純虛數的特徵根，且q相對於 適當小時，則(1)和(2)在原點附近解的漸近性態完全相同。設P有 個具有負實部的特徵根，而其餘具有正實部，又假定當 及 時，對 一致地有
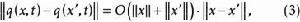按一次近似決定穩定性
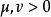按一次近似決定穩定性則存在常數 ，使得下述性質成立：
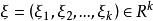按一次近似決定穩定性
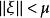按一次近似決定穩定性
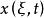按一次近似決定穩定性1. 當 且 時，(2)有連續依賴於ξ的解 ，使得
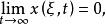按一次近似決定穩定性且原點關於這族解是漸近穩定的。
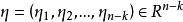按一次近似決定穩定性
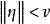按一次近似決定穩定性
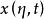按一次近似決定穩定性2. 當 且 時，(2)有連續依賴於η的解 ，使得
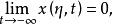按一次近似決定穩定性
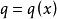按一次近似決定穩定性
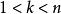按一次近似決定穩定性設(2)為自治的： ，且 ，則性質1和2表現的性質為典型的鞍點性質，它們給出了原點的局部穩定和不穩定流形 。
