基本介紹
多項式是逼近函式的一種常用的工具,在尋求函式極小點的區間上,可以利用在若干點處的目標函式值來構造一個多項式,作為目標函式的近似表達式,並用這個多項式的極小點作為原目標函式極小點的近似,重複套用這一方法進行疊代計算,直到得出滿意的結果為止,這種方法稱為 插值法。常用的插值法有線性插值(切線法)、三次插值法、二次插值法,前兩種方法均要進行導數計算,下面介紹比較簡單常用的二次插值法又稱 拋物線插值法 。
方法步驟
 拋物線插值法
拋物線插值法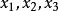 拋物線插值法
拋物線插值法設目標函式是連續的,三點滿足
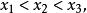 拋物線插值法
拋物線插值法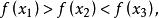 拋物線插值法
拋物線插值法構造拋物線
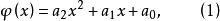 拋物線插值法
拋物線插值法使
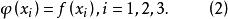 拋物線插值法
拋物線插值法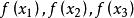 拋物線插值法
拋物線插值法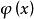 拋物線插值法
拋物線插值法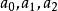 拋物線插值法
拋物線插值法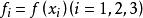 拋物線插值法
拋物線插值法只要不為同一值,則就是一確定的拋物線,其中係數可由條件(2)定出,若記,則式(2)變成
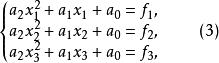 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法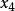 拋物線插值法
拋物線插值法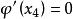 拋物線插值法
拋物線插值法設拋物線的極小點為,則應滿足,即
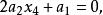 拋物線插值法
拋物線插值法因此
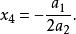 拋物線插值法
拋物線插值法利用克萊姆法則解方程組(3)並代入上式可得
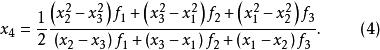 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法由於三點函式值滿足“兩頭高,中間低”,故由此決守的拋物線,其極小點自然落在區間之內,這在幾何上是明顯的。
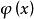 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法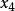 拋物線插值法
拋物線插值法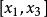 拋物線插值法
拋物線插值法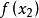 拋物線插值法
拋物線插值法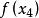 拋物線插值法
拋物線插值法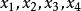 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法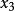 拋物線插值法
拋物線插值法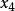 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法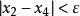 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法一般說來,僅通過一次工作,用拋物線代替求極小點,誤差可能較大。我們把作為搜尋區間的一個內點,通過比較與的大小,必可在中去掉或,使餘下的三點構成一個新的搜尋區間,且滿足函式值“兩頭高,中間低”的要求,再以這三個點為出發點,重複上述步驟,又可得到一個新的極小點的近似值。如此反覆進行,直到求得的極小點與已知三個點的中間一點滿足,即可終止疊代,為預先給定的正數。
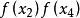 拋物線插值法
拋物線插值法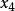 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法 拋物線插值法
拋物線插值法還應注意的是,在每一次疊代中比較以確定下一次搜尋區間時,拋物線極小點可能落在之左,也可能落在之右 。

