簡介
在數學中，拉梅函式（或橢球諧波函式）是拉梅方程（二階常微分方程）的解。 它在論文（加布里埃爾·拉梅1837）中介紹。 拉梅方程出套用於橢圓坐標中拉普拉斯方程的變數分離方法中。在一些特殊情況下，可以用稱為拉梅多項式的多項式來表示解。
拉梅方程的公式
拉梅方程的等式如下：
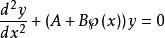拉梅方程
拉梅方程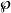
拉梅方程
拉梅方程其中A和B是常數，是魏爾斯特拉斯(Weierstrass)橢圓函式。 最重要的情況是當和對於整數n和k的橢圓模，在這種情況下，解擴展到在整個複平面上定義的擬態函式。對於B的其他值，解具有分支點。
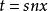拉梅方程通過用將獨立變數更改為t，拉梅方程也可以以代數形式重寫為
拉梅方程經過變化之後變成了亨恩方程的特例。
拉梅方程拉梅方程的更一般形式是可以寫入的橢圓方程或橢圓波方程（觀察我們寫的是，而不是上面的A）。
拉梅方程
拉梅方程
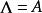拉梅方程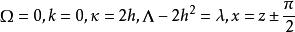
拉梅方程
拉梅方程其中k是雅可比橢圓函式的橢圓模量，是常數。 對於，方程式成為具有的拉梅方程。對於方程簡化為Mathieu方程
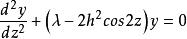拉梅方程拉梅方程的威爾斯特拉斯式非常不適合於計算。方程式最合適的形式是以雅可比形式。代數和三角形的使用也很麻煩。拉梅方程出現於量子力學中，作為關於各種周期性和非調諧電位的Schrödinger方程的經典解的小波動方程。
漸近展開
拉梅方程Müller已經獲得了對於κ的大值的周期性橢圓波函式的漸近展開，以及拉梅方程的漸近展開。他對於特徵值獲得的漸近展開是，q近似為一個奇整數（並且由邊界條件更準確地確定）：
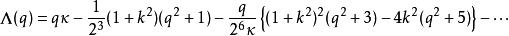拉梅方程觀察條件在q和k（如Mathieu函式的相應計算，扁圓球形波函式和扁圓球形波函式）中交替。具有以下邊界條件（其中K（k）是由完整橢圓積分給出的四分之一周期）
拉梅方程以及導數
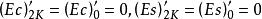拉梅方程分別定義橢球波函式
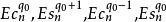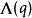拉梅方程
拉梅方程這裡的上標是指Ec的解，而較低的解Es。最後在q擴展，會得到：
拉梅方程
拉梅方程在Mathieu方程的極限中，這些表達式減少到Mathieu情況的相應表達式。
