內容
該理論包含兩個重要內容：均值－方差分析方法和投資組合有效邊界模型。
在發達的證券市場中，馬科維茨投資組合理論早已在實踐中被證明是行之有效的，並且被廣泛套用於組合選擇和資產配置。但是，我國的證券理論界和實務界對於該理論是否適合於我國股票市場一直存有較大爭議。
從狹義的角度來說，投資組合是規定了投資比例的一攬子有價證券，當然，單只證券也可以當作特殊的投資組合。本文討論的投資組合限於由股票和無風險資產構成的投資組合。
人們進行投資，本質上是在不確定性的收益和風險中進行選擇。投資組合理論用均值—方差來刻畫這兩個關鍵因素。所謂均值，是指投資組合的期望收益率，它是單只證券的期望收益率的加權平均，權重為相應的投資比例。當然，股票的收益包括分紅派息和資本增值兩部分。所謂方差，是指投資組合的收益率的方差。我們把收益率的標準差稱為波動率，它刻畫了投資組合的風險。
人們在證券投資決策中應該怎樣選擇收益和風險的組合呢？這正是投資組合理論研究的中心問題。投資組合理論研究“理性投資者”如何選擇最佳化投資組合。所謂理性投資者，是指這樣的投資者：他們在給定期望風險水平下對期望收益進行最大化，或者在給定期望收益水平下對期望風險進行最小化。
因此把上述最佳化投資組合在以波動率為橫坐標，收益率為縱坐標的二維平面中描繪出來，形成一條曲線。這條曲線上有一個點，其波動率最低，稱之為最小方差點（英文縮寫是MVP）。這條曲線在最小方差點以上的部分就是著名的（馬考維茨）投資組合有效邊界，對應的投資組合稱為有效投資組合。投資組合有效邊界一條單調遞增的凹曲線。
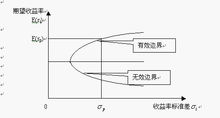投資組合理論如果投資範圍中不包含無風險資產（無風險資產的波動率為零），曲線AMB是一條典型的有效邊界。A點對應於投資範圍中收益率最高的證券。
如果在投資範圍中加入無風險資產，那么投資組合有效邊界是曲線AMC。C點表示無風險資產，線段CM是曲線AMB的切線，M是切點。M點對應的投資組合被稱為“市場組合”。
如果市場允許賣空，那么AMB是二次曲線；如果限制賣空，那么AMB是分段二次曲線。在實際套用中，限制賣空的投資組合有效邊界要比允許賣空的情形複雜得多，計算量也要大得多。
在波動率－收益率二維平面上，任意一個投資組合要么落在有效邊界上，要么處於有效邊界之下。因此，有效邊界包含了全部（帕雷托）最優投資組合，理性投資者只需在有效邊界上選擇投資組合。
產生髮展
現代投資組合理論主要由投資組合理論、資本資產定價模型、APT模型、有效市場理論以及行為金融理論等部分組成。它們的發展極大地改變了過去主要依賴基本分析的傳統投資管理實踐，使現代投資管理日益朝著系統化、科學化、組合化的方向發展。
1952年3月，美國經濟學哈里·馬考威茨發表了《證券組合選擇》的論文，作為現代證券組合管理理論的開端。馬克威茨對風險和收益進行了量化，建立的是均值方差模型，提出了確定最佳資產組合的基本模型。由於這一方法要求計算所有資產的協方差矩陣，嚴重製約了其在實踐中的套用。
1963年，威廉·夏普提出了可以對協方差矩陣加以簡化估計的單因素模型，極大地推動了投資組合理論的實際套用。
20世紀60年代，夏普、林特和莫森分別於1964、1965和1966年提出了資本資產定價模型（CAPM）。該模型不僅提供了評價收益一風險相互轉換特徵的可運作框架，也為投資組合分析、基金績效評價提供了重要的理論基礎。
1976年，針對CAPM模型所存在的不可檢驗性的缺陷，羅斯提出了一種替代性的資本資產定價模型，即APT模型。該模型直接導致了多指數投資組合分析方法在投資實踐上的廣泛套用。
其他論述
（portfolio theory)
投資組合理論風險管理的數量分析。
投資組合理論被定義為最佳風險管理的定量分析。無論分析的單位是家庭、公司，還是其他經濟組織，為了找到最優的行動方案，需要在減少風險的成本與收益之間進行權衡，對這些內容闡述並估計的過程，即投資組合理論的套用。
對家庭而言，消費和風險偏好是已知的。偏好會隨著時間而改變，但這些變化的機制和原因並非投資組合理論闡述的內容。投資組合理論闡述了如何在金融工具中進行選擇，以使其特定的偏好最大化。通常，最佳選擇包括對獲取較高預期回報和承擔較大風險之間權衡的評估。
套用問題
馬考威茨的投資組合理論不但為分散投資提供了理論依據，而且也為如何進行有效的分散投資提供了分析框架。但在實際運用中，馬考威茨模型也存在著一定的局限性和困難：
1．馬考威茨模型所需要的基本輸入包括證券的期望收益率、方差和兩兩證券之間的協方差。當證券的數量較多時，基本輸入所要求的估計量非常大，從而也就使得馬考威茨的運用受到很大限制。因此，馬考威茨模型目前主要被用在資產配置的最優決策上。
2．數據誤差帶來的解的不可靠性。馬考威茨模型需要將證券的期望收益率、期望的標準差和證券之間的期望相關係數作為已知數據作為基本輸入。如果這些數據 沒有估計誤差，馬考威茨模型就能夠保證得到有效的證券組合。但由於期望數據是未知的，需要進行統計估計，因此這些數據就不會沒有誤差。這種由於統計估計而帶來的數據輸入方面的不準確性會使一些資產類別的投資比例過高而使另一些資產類別的投資比例過低。
3．解的不穩定性。馬考威茨模型的另一個套用問題是輸人數據的微小改變會導致資產權重的很大變化。解的不穩定性限制了馬考威茨模型在實際制定資產配置政策方面的套用。如果基於季度對輸人數據進行重新估計，用馬考威茨模型就會得到新的資產權重的解，新的資產權重與上一季度的權重差異可能很大。這意味著必須對資產組合進行較大的調整，而頻繁的調整會使人們對馬考威茨模型產生不信任感。
4．重新配置的高成本。資產比例的調整會造成不必要的交易成本的上升。資產比例的調整會帶來很多不利的影響，因此正確的政策可能是維持現狀而不是最最佳化。
