托密勒定理

托密勒定理，是指在圓內接四邊形中，兩條對角線長度的積等於它的兩組對邊乘積的和。

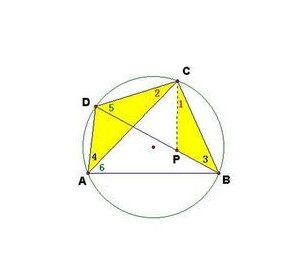
證明圖

托密勒定理是如果圓有內接四邊形，則四邊形對邊乘積之和等於對角線的乘積。

求證

在圓內接四邊形中，兩條對角線長度的積等於它的兩組對邊乘積的和,即AB*CD+AD*BC=AC*BD。

證明:過C作CP交BD於P,使∠1=∠2,又∠3=∠4,

∴△ACD∽△BCP.

又∠ACB=∠DCP,∠5=∠6,

∴△ACB∽△DCP.

有：DC/AC=DP/AB AC*DP=AB*DC(1）

AD/BP=AC/BC BP*AC=AD*BC（2）

①+②得 AC(BP+DP)=AB·CD+AD·BC.

即AC·BD=AB·CD+AD·BC.